Expansion de l’univers
On observe que toutes les galaxies s’éloignent les unes des autres d’autant plus rapidement qu’elles sont éloignées, que la lumière émise des objets est d’autant plus décalée vers le rouge qu’ils sont éloignés et que l’intervalle entre deux évènements subit également une dilatation temporelle. On interprète tous ces phénomènes en faisant l’hypothèse que l’espace est en « expansion », dans le cadre de la métrique de Robertson-Walker.
Les phénomènes décrits ont un caractère objectif et le propos n’est pas de les remettre en cause.
Mais, au-delà du caractère mystérieux de cette phénoménologie (un espace qui se dilate), ceci s’appuie sur un feuilletage de l’espace-temps, en temps et espace, particulier qui, même s’il est judicieux, est arbitraire. On sait qu’en relativité, temps et espace pris séparément n’ont pas de caractère physique, celui-ci étant l’apanage de l’espace-temps.
De toute façon, il n’y aurait pas plus de raison d’attribuer un caractère physique à l’espace défini de cette manière qu’à un autre défini en fonction d’un autre feuilletage.
Cette interprétation est donc critiquable, car elle ne semble valide dans ce type de feuilletage.
Une autre manière, plus conforme à la relativité générale, de décrire cette phénoménologie est de dire que les objets célestes décrivent les géodésiques définies par l’équation d’Einstein, ce qui est indéniable, et que cette structure particulière est une propriété « interne » de l’espace-temps et non pas de l’espace, et que si nous observons ces propriétés dans l’espace (qui serait en expansion), cela est dû au processus expérimental d’observation et à son interprétation. Ceci est explicité dans le livre « Vous avez-dit Big- Bang ».
Accélération de l’expansion : constante cosmologique
Cette accélération qu’on constate expérimentalement est généralement imputée (cela n’a rien de définitif, mais pour l’instant c’est l’hypothèse la plus conforme aux constats expérimentaux) à la présence d’une constante cosmologique dans l’univers qu’on essaie de justifier par « l’énergie du vide » malgré une énorme différence d’échelle. Nous discutons de cette différence dans d’autres articles sur ce site, notamment à propos de la force de Planck.
Si l’interprétation physique est encore sujette à caution, il faut bien préciser le contexte géométrique, car rappelons que la relativité qui sous-tend la cosmologie est une théorie géométrique de la gravitation.
Expansion de l’univers ou divergence des géodésiques dans la variété représentant l’univers?
La constante cosmologique seule définit un espace-temps à quatre dimensions à symétrie maximale (10 symétries), nulle elle correspond à l’espace-temps de Minkowski (relativité restreinte), positive à un espace-temps de De Sitter et négative à un espace-temps d’anti- De Sitter.
Ils sont tous des espace-temps où la courbure spatio-temporelle, représentée par le scalaire de Ricci est constante.
Ceci implique que le tenseur de Riemann, dépendant de la métrique et de ses dérivées premières et seconde dont le scalaire de Ricci est issu par une double contraction a une fourme bien particulière: il ne comporte aucune dérivée de la métrique. Sans rentrer dans les détails c’est la différence de 2 produits tensoriels de la métrique. La métrique est décrite dans des coordonnées dont une de type temps est de signe contraire (dans la métrique) à celles de type espace.
On comprend alors que pour que l’expression reste constante quand on parcoure une ligne d’univers où le temps est croissant, l’espace de signe contraire doit aussi croître pour maintenir la courbure constante. Bien sur il faut faire le calcul, avec la formule mathématique qui décrit ces expressions, pour s’en persuader, l’argument ayant un caractère analogique pour le phénomène.
Certes, en faisant ainsi, on procède par analogie pour décrire le phénomène. Il faut faire le calcul, avec la formule mathématique qui décrit ces expressions, pour s’en persuader.
La congruence de géodésiques caractérise la structure interne de l’univers
Nous allons montrer par un calcul simple comment montrer que, plutôt que de parler d’expansion de l’univers, il faut considérer cela comme une propriété interne à cet univers.
Pour cela nous allons considérer la congruence de géodésiques dans la métrique de Robertson-Walker. Cette congruence décrit comment un faisceau de géodésiques, autour et au voisinage d’une géodésique « directrice », se comportent quand le paramètre affine de la géodésique « directrice » varie. Ceci décrit la structure interne de la géométrie de la variété représentant l’espace-temps, car ce que décrit essentiellement l’équation d’Einstein, c’est la dynamique de la gravitation (le « mouvement ») caractérisée par les géodésiques dans cette théorie géométrique de la gravitation.
Pour une orientation donnée de la variation, sa section circulaire peut varier (expansion/contraction), se déformer (cisaillement) ou tourner (rotation). Ces informations sont décrites par des paramètres, en particulier la paramètre d’expansion (ou contraction), généralement désigné θ, de la congruence qui est un scalaire et qui est le seul paramètre non nul, dans cette forme de métrique. Il s’écrit :
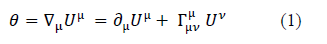
Le signe « nabla » (triangle sur la pointe) représente la dérivée covariante. L’équation (1) ’est la divergence covariante du 4-vecteur géodésique Uµ de composantes (t, r, θ, φ), conventionnellement notées respectivement, 0, 1, 2, 3, dont les composantes sont :
Uµ = {1, 0, 0, 0} (2)
Dans ces conditions, comme seul U0 n’est pas nul, l’équation (1) s’écrit :
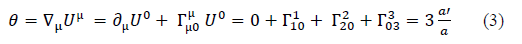
La dérivée partielle de U0est nulle car U0 = 1, et les symboles de Christoffel valent :
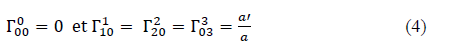
Et a’ désigne la dérivée de a(t) par rapport à t. En prenant, par exemple, la solution donnée par les équations de Friedmann avec k = 0 :
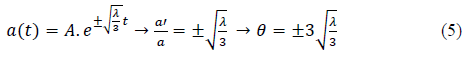
Cette expansion θ, constante dans le cas d’un univers de De Sitter est donc, intrinsèquement, de caractère géométrique, c’est une propriété interne à cette géométrie, indépendamment de toutes les interprétations physiques qu’on peut envisager.
On voit que cette expansion constante des géodésiques conduit à une expansion de type « exponentiel »
Cas d’un univers non vide
Quand il y a de la matière énergie dans l’univers (matière froide, matière relativiste et rayonnement), on peut se demander vers quoi tend l’univers lorsque cette quantité de matière énergie tend vers zéro pour chercher quelle structure géométrique « nue » serait la trame d’un tel espace-temps.
L’hypothèse habituelle est que la courbure est nulle donc qu’un espace-temps tendrait vers l’espace-temps de Minkowski lorsque la matière-énergie tend vers zéro.
Mais elle peut tout aussi bien tendre vers un espace de De Sitter ou anti-De Sitter qui a le même niveau de symétrie. Y-a-il une raison pour privilégier l’une ou l’autre solution ?
Par exemple si la constante cosmologique s’avère être la bonne solution pour notre univers, il n’y a pas matière à s’étonner, les 3 solutions se valent…
Inflation primordiale
Ce paradigme, plutôt bien intégré aujourd’hui dans le modèle cosmologique, suppose que, très tôt dans l’histoire de l’univers, une croissance de type exponentiel a eu lieu pendant un temps égal à au moins 100 fois l’âge de l’univers, au moment où elle s’est produite.
Ceci permet d’expliquer un certain nombre de phénomènes constatés sur l’homogénéité de l’univers, le problème de l’horizon, la courbure quasi nulle de la section spatiale dans la métrique de Robertson-Walker et l’absence de monopoles magnétiques.
Le problème de l’horizon
L’étude du RFC (rayonnement de fond cosmologique) montre qu’il est très homogène (les inhomogénéités sont de l’ordre de 10-5) . Dans un milieu, un gaz par exemple, l’homogénéité résulte des nombreuses collisions entre les atomes ce qui amène à un équilibre thermique qui suit une loi de type corps noir.
Pour cela, il faut que les différentes parties de l’univers aient été en contact. Sans cette inflation, dans le modèle standard, sauf conditions initiales très particulières, ceci semble impossible.
Notons qu’il s’agit d’un phénomène à caractère physique puisque c’est la limite au-delà de laquelle où plus aucun signal ne nous parvient. Dans un univers dynamique cette limite dépend du temps cosmologique, à contrario de l’horizon dans la solution de Schwarzschild avec trou noir où elle est fixe.
Le problème de la platitude de l’espace
Un argument avancé est que pour rendre compte de cette quasi-nullité de cette courbure, il aurait fallu des conditions initiales extraordinairement particulières, donc extraordinairement peu probables.
L’argument est intéressant, mais il faut faire remarquer que la « platitude » de la section spatiale d’un espace-temps n’a rien d’universel, car cet espace dépend du feuilletage de l’espace-temps en temps et espace qui dépend-lui même des coordonnées.
Ainsi, pour un espace-temps de De Sitter par exemple, il existe des solutions où la section spatiale est à courbure positive, négative ou nulle, pour le même espace-temps, (décrit mathématiquement par la même variété), certaines couvrant toute la variété d’autres seulement une partie, ceci dépendant de coordonnées.
On peut donc être dubitatif sur la valeur intrinsèque et l’importance de cette courbure nulle pour la section spatiale qui n’a pas de caractère physique.
L’intérêt qu’on lui portait, dans les solutions sans constantes cosmologiques était sans doute lié au fait que le destin de l’univers dépendait de cette courbure (fermé, ouvert, asymptotiquement infini). Mais avec la constante cosmologique, la donne a changé.
Validation du paradigme de l’inflation
Pour être validé ce paradigme doit faire l’objet de vérifications expérimentales.
S’il est vrai qu’il résout plusieurs problèmes, pour les conditions initiales extraordinairement particulières on peut faire observer que le Big Bang est lui même un évènement pas vraiment ordinaire et que si on l’accepte, on pourrait ne pas s’étonner qu’il s’accompagne d’un autre évènement du même acabit.
Il apparait que ce paradigme a connu de nombreuses versions depuis le début et que de nombreuses variantes existent et font partie de travaux de recherche, aujourd’hui .
Le médiateur quantique du champ scalaire « l’inflaton » est inconnu et si on a pensé que ce pouvait être le boson de Higgs, cette hypothèse semble abandonnée aujourd’hui.
De plus le profil et les propriétés du champ scalaire associé à l’inflation exigent d’importantes contraintes pour représenter le phénomène tel qu’on le décrit, ce qui fait dire que si des contraintes aussi fortes que celles initiales requises pour un univers de géométrie spatiale plate, on ne voit pas bien l’intérêt d’ajouter ce paradigme, sauf s’il résout des problèmes que l’ajustement fin des paramètres initiaux ne résout pas (problème de l’horizon, homogénéité, spectre des fluctuations, absence de monopoles magnétiques).
Il est certain que tous ces points donnent du crédit à l’inflation, mais la confusion actuelle et la pléthore de variantes montrent que l’histoire est loin d’être terminée. Seule une vérification expérimentale non ambigüe lèverait l’hypothèque sur ce paradigme.