Espaces à symétries maximum[1]

Chapitre 1 : Problème à résoudre – généralités sur les symétries des espaces

Quel niveau de symétries pour un espace ? Un espace à n dimensions Rn de métrique euclidienne est invariant par les translations et rotations autour de tout point P.

Il y a n translations linéairement indépendantes et comme il y a n axes de rotations, autour de chaque axe considéré il y a n-1 rotations des autres axes, mais compte tenu qu’une rotation de x vers y est la même que y vers x il faut diviser l’ensemble par 2. Ceci fait donc : ½ n(n-1) rotations.

Au total cela fait :  n + ½ n(n-1) = ½ n(n+1)

En espace de Minkowski de signature Lorenztienne, certaines rotations sont des boosts.

Pour des espaces non euclidiens, il existe des espaces comme la sphère, et les hypersphères qui sont aussi à symétrie maximum, ainsi que leurs équivalents de type hyperbolique.

Si la variété non euclidienne représentant l’espace-temps est à symétrie maximum sa courbure doit être la même partout et dans toutes les directions (homogène et isotrope). Si nous la connaissons en un point alors nous la connaissons pour tous les points. Il y a peu d’espaces à symétrie maximale.

***********************************************************************

Quelques rappels :

Le tenseur de Riemann s’écrit :

R^ρ_σμν = ∂_μΓ^ρ_νσ – ∂_νΓ^ρ_μσ + Γ^ρ_μλΓ^λ_νρ – Γ^ρ_νλΓ^λ_μσ

Où Γ^λ_µν est un symbole de Christoffel qui vaut :

Γ^λ_µν = ½ g^λσ(∂_μg_νσ +∂_νg_σμ – ∂_σg_μν)

Où g_μν est la métrique et g^λσ la métrique inverse définie par :

g^µρ.g_ρν= δ^µ_ν

Où δ^µ_ν est le symbole de Kronecker qui vaut 1 pour µ = ν et zéro sinon.

Rappelons que la métrique et la métrique inverse permettent respectivement d’abaisser et d’élever des indices dans les tenseurs. Ainsi la version du tenseur de Riemann avec tous les indices bas s’écrit :

R_λσμν = g_λρR^ρ_σμν

On doit sommer sur l’indice ρ de 0 à 3 sur son expression pour réaliser l’opération.

Le tenseur de Ricci R_µν qui est la contraction du tenseur de Riemann s’écrit :

R_µν = R^ρ_µρν

Conformément à la notation d’Einstein, on contracte en sommant sur l’indice ρ de 0 à 3.

Quant au scalaire de Ricci R, il vaut :

R = R^µ_µ = g^µν R_µν

***********************************************************************

Les variétés à symétrie maximale sont classées par la valeur du scalaire de courbure de Ricci R qui sera constant partout, le nombre de dimensions n, la signature de la métrique et la topologie (distinguer un n-tore de l’espace euclidien Rn).

Pour de tels espaces nous pouvons reconstruire le tenseur de Riemann à partir du scalaire de Ricci R

Solution proposée

L’idée est que, comme la géométrie est la même dans toutes les directions, le tenseur de courbure doit être le même dans toutes les directions. Comment faire ? Choisissons des coordonnées locales (indices en gras) inertielles à un point P telles que g_µν = η_µν . Ces coordonnées locales ne sont pas uniques.

Comme la géométrie est à symétrie maximale imposons que les composantes du tenseur de Riemann soient de même et qu’elles ne doivent pas changer par application d’une transformation de Lorentz.

Il n’y a que peu de tenseurs qui ont cette propriété, la métrique, le tenseur de Kronecker et celui de Levi-Civita. Cela implique que le tenseur de Riemann, dans ces coordonnées doit être proportionnel à un tenseur construit à partir de ces tenseurs invariants.

Comme ce tenseur doit respecter les symétries intrinsèques du tenseur de Riemann[2], la seule solution est :

R_ρσμν = k. (g_ρμ g_σν – g_ρν g_σμ)

Où k est un facteur de proportionnalité.

Vérifions, par exemple, que cette solution satisfait bien à l’antisymétrie par permutation sur les 2 premiers indices (ρ↔σ) du tenseur de Riemann

R_σρμν = k. (g_σμ g_ρν – g_σν g_ρμ) = – R_ρσμν = k. (g_ρμ g_σν – g_ρν g_σμ)

Vous pouvez vérifier à titre d’exercice que les autres « symétries » sont bien réalisées.

Comme cette relation est tensorielle, elle est valide dans n’importe quelles coordonnées.

Calcul de la constante de proportionnalité

Quelques rappels :

On utilise la convention d’Einstein pour la contraction des tenseurs (qui réduit leur ordre) un indice haut se contracte avec un indice bas de même nom, de dimension n, selon la loi :

A^µ_ν B_µρ = C_νρ = A⁰_ν B_0ρ + ..+ Aⁿ_ν B_nρ

On rappelle qu’on utilise la convention d’Einstein, il faut donc sommer sur ρ.

Avec ces précisions, on doit être capable de comprendre la suite.

On peut facilement calculer la constante de proportionnalité en contractant les 2 termes de la relation ce qui se fait comme suit :

g^ρμR_ρσμν  = k. g^ρμ(g_ρμ g_σν – g_ρν g_σμ)

g^ρμR_ρσμν  = k. g^ρμ(g_ρμ g_σν – g_ρν g_σμ)

On va d’abord élever le premier indice puis contracter sur cet indice

R^µ_σμν  = R_σν = k. g^ρμ(g_ρμ g_σν – g_ρν g_σμ) = k. (n g_σν – δ^µ_ν g_σμ)= k. (n g_σν – g_σν)

Puis pour obtenir le scalaire de Ricci on va contracter une deuxième fois.

g^ρσ R_σν = R = k. (n -1) g^ρσ g_σν = k. (n -1)n → k = R/[(n(n-1)]

Le terme de gauche devient R et celui de droite n(n-1).

On obtient alors :

R_ρσμν = R/[n(n-1)] (g_ρμ g_σμ – g_ρν g_σμ)

Espaces temps à symétrie maximum^[3]

Les espaces temps à symétrie spatiale maximum sont en fait des cas particuliers d’une situation plus générale où, par exemple, c’est seulement l’espace qui est symétrique.

Dans un certain sens, de tels univers sont des « états de base » de la Relativité Générale.

Le tenseur de Riemann caractérise complètement la courbure intrinsèque de l’espace- temps, il doit donc refléter ses symétries. 

Dans le cas général, ses composantes sont des fonctions de la métrique et de ses dérivées premières et secondes.

Pour un espace-temps à symétrie maximum, il se simplifie considérablement, ses composantes ne sont fonction de que la métrique elle-même. Dans une variété à n dimensions de métrique g_µν, il s’écrit :

R_ρσµν =K(g_ρµg_σν – g_ρνg_σµ)                                                                   (4.1)

Où K est la mesure normalisée de la courbure de Ricci

K = R/n(n-1)   = R/12             (pour n =4)                                       (4.2)

Et le scalaire de Ricci « R » doit être constant partout dans la variété. Comme nous pouvons toujours mettre la métrique sous sa forme canonique en un point quelconque (g_µν = η_µν), les sortes d’espaces temps à symétrie maximum vont être caractérisés localement par la signature de la métrique et par le signe du paramètre constant K.

Nous disons, localement, pour permettre différentes solutions globales possibles, comme pour le plan et le tore.

Nous nous intéressons aux métriques de signatures (- + + + ).

Les trois cas génériques correspondent donc à K < 0 (espace-temps anti De Sitter) , K = 0 (espace-temps de Minkowski) , K > 0 (espace-temps de De Sitter)

Pour K = 0 nous connaissons bien cette métrique, c’est celle de Minkowski.

ds² = -dt² + dx² + dy² + dz²                                                                (4.3)

Le diagramme conforme associé est connu. C’est l’espace-temps de la relativité restreinte. Nous ne développerons pas ce cas.

L’espace-temps à symétrie maximum correspondant à K > 0, courbure positive^[4] est appelé l’espace « de Sitter ».

Considérons un espace de Minkowski à 5 dimensions de métrique

ds₅²= -du² + dx² + dy² + dz² + dw² et définissons y un (hyper)hyperboloïde^[5] donné par

-u² + x² + y² + z² + w² = α²                                                                (4.4)

Maintenant définissons les coordonnées ( t, χ, θ, Ф)sur  l’(hyper)hyperboloïde via

u = α.sinh(t/α)

w = α.cosh(t /α).cosχ

x = α.cosh(t/α).sinχ.cosθ

y = α.cosh(t/α).sinχ.sinθ.cosФ

z = α.cosh(t/α).sinχ.sinθ.sinФ                          (4.5)

La métrique sur l’hyperboloïde est alors

ds² = -dt² + α²cosh²(t/α)[ dχ² + sin²χ(dθ² +sin²θdФ²)]                     (6)

1. La métrique est non statique. Mathematica 4, permet de vérifier qu’elle satisfait (4.1).

• Il n’y a pas de singularité apparente (mais un horizon des évènements^[6]). A ce propos, remarquons que quand nous avons calculé la distance de cet horizon pour les formes (4)-(5), nous avons noté qu’elle dépendait des coordonnées temporelles de l’observateur (cette distance est maximum pour t = 0 et elle → 0 quand t → ∞ où l’univers devient totalement causalement déconnecté).

On peut vérifier que ceci s’applique également à la forme (6). Cela peut paraître surprenant pour une solution a symétrie maximum où tous les points sont équivalents.  A priori, un système de coordonnées étant arbitraire, il semblerait toujours possible d’imposer t = 0 et ψ = 0 pour l’observateur qu’on considère (choix des origines). 

Mais remarquons que les formes (4)-(6) n’étant pas homogènes par rapport au temps, elles déterminent des classes d’observateurs et la dépendance des coordonnées doit se lire comme caractérisant la relation entre les différentes classes.

Cela est lié à la brisure de symétrie liée à l’utilisation de cette forme. Existe-t-il cependant un critère indépendant des coordonnées, de nature conforme, par exemple, lié aux géodésiques nulles, pour caractériser les hypersurfaces remarquables qui régentent la causalité ?

L’équivalence conforme entre l’univers de De Sitter et celui statique d’Einstein, n’éclaire pas ce problème comme on aurait pu l’espérer, car il n’y a pas d’horizon des évènements dans la solution statique d’Einstein.

.

• La coordonnée t correspond au temps propre.

• Nous reconnaissons^[7] entre parenthèses la métrique sur une 2-sphère dΩ₂² et entre crochets la métrique sur une 3-sphère dΩ₃² qui sont les sections spatiales.

• Le scalaire de Ricci vaut 12/α² conformément à (4-2) avec α² =1/K, α étant le rayon de l’hypersphère spatiale : il est constant sur la variété (vérifié par mathématica 4).

• La forme décrit une variété spatialement ouverte cosh(t/α) → ∞ quand t → ± ∞.

• Ces coordonnées couvrent toute la variété. On peut le vérifier en étudiant le comportement des géodésiques aux limites du système de coordonnées, car si les coordonnées sont incomplètes, les géodésiques se terminent alors que le paramètre affine associé reste fini

La topologie de l’espace « de Sitter » est R x S³.

Donc la métrique de « de Sitter » décrit une 3-sphère qui initialement rétrécit, atteint son minimum pour t = 0, et ensuit rebondit et gonfle à jusqu’à l’infini.

L’univers de De Sitter et l’univers statique d’Einstein sont conformément équivalents

Il y correspond un diagramme conforme très simple, on peut en effet écrire cette métrique dans une forme conformément reliée à l’univers statique d’Einstein (un espace-temps de topologie R x S3, décrivant une 3-sphère spatiale de rayon constant dans le temps). Considérons la transformation de coordonnée de t en t’ par :

cosh(t/α) = 1/cos(t’)                                                               (4.7)

La métrique (4.6) devient alors

ds² = [ α²/cos²(t’)] ds’²                                                           (4.8)

Où ds’² représente la métrique de l’univers statique d’Einstein

            ds’² = -dt’² +dχ² +sin²χ.dΩ₂²                                                 (4.9)

la nouvelle coordonnée temps s’étend de

-π/2 < t’< π/2                                                             (4.10)

Ceci est représenté par le diagramme ci-dessous.

Le diagramme conforme de l’espace-temps « de Sitter » est simplement la représentation de la pièce de l’univers statique d’Einstein, qui y est conformément équivalent.

Il ressemble à un carré, comme la figure 4.1 le montre.

Une tranche d’espace à t’constant représente une 3-sphère (hypersphère), les lignes interrompues à gauche et à droite sont le pôle nord et le pôle sud de cette 3-sphère.

Les lignes diagonales représentent des trajectoires de photons.

Un photon partant de l’infini du passé va aller à l’antipode de cette 3 sphère à l’infini du futur.

Si l’hypersphère n’est pas facile à se représenter, il faut se rappeler que les géodésiques lumière suivent des grands cercles de l’hypersphère, qui sont eux faciles à représenter, c’est pour cela que à l’image de ce qui se passe à la surface d’une 2-sphère pour des grands cercles un photon va aux antipodes (et il peut continuer et boucler indéfiniment dans la solution d’univers statique d’Einstein).

Par ailleurs la représentation conforme préserve le caractère des géodésiques lumières, et la causalité associée.

Gardons à l’esprit que l’espace se « termine » dans le passé et dans le futur par la « magie » de la transformation conforme, l’espace-temps de « de Sitter » s’étendant indéfiniment vers le passé et vers le futur.

Remarquons aussi que deux points peuvent avoir des cônes de lumière du futur ou du passé qui sont complètement disjoints.

Ceci est dû au fait que les sections sphériques spatiales s’étendent si rapidement que la lumière d’un point ne peut jamais rencontrer celle émise par l’autre.

Le fait que ces univers soient conformément équivalents n’est pas surprenant car ils sont tous les deux à symétrie maximum, ceci malgré leur différence de nature physique, l’univers statique d’Einstein contient de la matière, il est fini et à ce titre a toutes les qualités requises par Einstein pour satisfaire au principe de Mach, alors que l’univers de De Sitter est vide.

Exemple d’espace à symétrie maximale : calcul de la métrique spatiale de Robertson-Walker

 

Compléments historiques sur l’espace-temps de De Sitter

Résumé:

Concernant la solution originale proposée par De Sitter, on montre que lorsqu’on procède à un changement de coordonnées pour faire disparaître la singularité, manifeste dans cette solution statique de l’espace-temps de « De Sitter », il demeure un horizon des évènements que des géodésiques traversent dans les deux sens ce qui éclaire la vraie nature de cette « pseudo singularité ».

On montre également que la solution de De Sitter qui malmène le principe de Mach, cher à Einstein, se révèle être une solution générale liée aux symétries du tenseur de Riemann, qu’on peut établir indépendamment des équations d’Einstein et de la métrique, (respecte la covariance).

Elle correspond à une variété à symétrie maximum, homogène, dont le scalaire de Ricci caractérisant la courbure (à quatre dimensions) est positif et constant sur toute la variété. Elle fait partie des trois solutions d’espace-temps à quatre dimensions de signature Lorentzienne à symétrie maximum dont les deux autres sont l’espace-temps anti De Sitter pour R < 0 et l’espace- temps de Minkowski pour R = 0.

Elle satisfait l’équation d’Einstein, mais n’est formellement en rien contrainte par elle. Ces solutions à symétrie maximum sont quelquefois appelées états de base de la relativité générale.

La « dynamique » de cette solution se comprend aisément. Brisons la covariance en étudiant qualitativement le comportement spatial et temporel. La courbure scalaire de Ricci (4D) étant constante quand la courbure spatiale est faible (grand rayon de l’hypersphère spatiale) la courbure temporelle (l’accélération) doit être forte et vice versa.

Mais est-ce vraiment une dynamique, ou simplement une exploration de la variété au moyen d’un système de coordonnées ?

Ceci nous amènera à réfléchir sur ce qui relève de propriétés purement géométriques et sur ce qui relève de l’équation d’Einstein.

Formes Statiques[8] de De Sitter et variantes : 1917-1918

La forme statique de De Sitter

Alors qu’Einstein était amené à modifier son équation fraîchement établie, en ajoutant en 1917 la constante cosmologique, pour trouver une solution d’univers statique dans le contexte cosmologique, De Sitter lui fit part d’une solution vide de matière à ses équations :

ds²= – cos²(r/R).dt² + dr² +R²[sin²(r/R)(dθ² + sin²θ.dφ²)]                                     (1.1)[9]

Einstein lui répondit dans un premier temps qu’un univers sans matière était inconcevable, mais cela allait ouvrir une polémique qui allait être de plus stigmatisée par la présence d’une singularité dans la forme proposée par De Sitter.

La forme (1.1) est manifestement singulière (le déterminant s’annule) à r = πR/2 où,pour des géodésiques radiales nulles, dr/dt =0

Cette singularité, très mal comprise a donné lieu à de longs débats entre Einstein, de Sitter, Klein, Weyl, Lancros, Lemaître, Robertson et quelques autres[10]. Deux points de vue s’affrontaient sur la nature de la singularité et l’existence d’une masse à l’horizon (pour satisfaire au principe de Mach).

Pour une description historique du débat se référer à Earman J. & Eisenstaedt J. (1999)

Comme le cite Klein[11], Weyl [12] avait déclaré : «la vitesse de la lumière s’annule sur l’équateur de la sphère et la forme de la métrique de l’univers de De Sitter doit donc être singulière ».

Effectivement pour une géodésique radiale nulle dr/dt =0 à l’équateur, mais Weyl a une vision confuse de cette singularité et ne tire pas les bonnes conclusions de sa remarque.

Les travaux ultérieurs vont éclairer la nature de cette singularité. Par ailleurs :

– Cette forme est statique : Les observateurs à coordonnées spatiales constante sont statiques.

– La coordonnée temps correspond au temps propre de l’observateur pour r = 0.

– Pour r =0, on se ramène à la forme de Minkowski.

– Les sections spatiales (à t = constante) sont l’hypersphère de rayon R.

Variantes de la forme statique de De Sitter

ds² = -(1-r²/R²).dt² + (1 –r²/R²)^-1.dr² + r².(dθ² + sin²θ.dφ²)                       (1.2) [13]

La singularité est à r =R (équateur) dans ces coordonnées.

A noter la ressemblance de cette forme (1.2) avec celle de Schwarzschild si on fait (r²/R² → R/r) où R serait le rayon de Schwarzschild. La coordonnée temps tend vers le temps propre pour r→ ∞ pour Schwarzschild au lieu de pour r→ 0 pour cette forme (1.2).

Citons une variante également statique où on utilise l’angle de développement χ = r/R à la place de r comme variable, par exemple, celle donnée par Einstein[14] qui est singulière pour χ  = π/2 ce qui correspond à l’équateur de l’hypersphère (r = π.R/2).

ds²= cos²χ.dt² – R² [dχ² +sin²χ (dθ² + sin²θ.dφ²)]                                                    (1.3)

Toutes ces variantes ont globalement les mêmes propriétés que la forme de De Sitter

Forme non statique de Lancros : 1922

En s’inspirant des travaux de Klein, Lancros[15] établit la forme suivante :

ds²= -dτ² + cosh²τ (dψ² + sin²ψ (dθ² + sin²θ.dφ²))                                     (2.1)[16]

τ est le temps propre des observateurs à coordonnées spatiales constantes (« comobiles »).

Klein[17] a cherché une forme en imbriquant l’espace-temps de « De Sitter » en l’occurrence un Hyper-hyperboloïde d’équation : -u² +x² + y² + z² + w² = a², dans un espace de Minkowski à 5 dimensions (quatre d’espace et une de temps) de métrique ds₅² = -du² + dx² + dy² + dz² +dw².

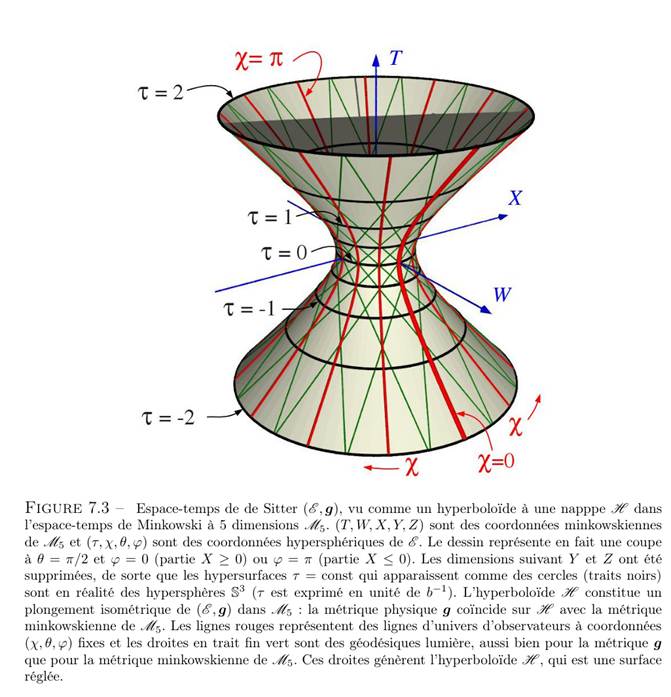
a) Il n’y a pas de singularité apparente, mais un calcul simple (ci-dessous) montre qu’il a un horizon des évènements associé à chaque observateur.

Pour illustrer une comparaison avec l’horizon de la forme de De Sitter (1.3) il faut étudier la même trajectoire d’un photon (géodésique nulle) émis par un observateur dans les deux systèmes de coordonnées qu’on va appliquer simultanément sur la variété. Fixons les coordonnées de l’observateur dans les deux formes. Il est naturel de faire coïncider le point (χ = 0, t =0) dans (1.3) avec (ψ =0, τ =0) dans (2.1) par raison de symétriedes formes.

Dans ces conditions le calcul montre que l’horizon dans (2.1) se situe à ψ = π/2, alors que la singularité exprimée par la forme (1.3) se situe à χ = π/2. On note la parfaite concordance.

b) Comme on le remarque, la forme (2.1) n’est plus statique (dépend du temps propre).

c) Les observateurs « comobiles » sont en chute libre, puisque la coordonnée temps est le temps propre.

d) Les sections spatiales sont des hypersphères de rayon dépendant du temps (S³).

e) Contrairement à (2.1-.3), la solution est spatialement ouverte (cosh²τ→ ∞ quand τ→ ± ∞).

f) La forme décrit toute la variété (extension analytique maximale)

—————————————————————————————————————–

Calcul du rayon de l’horizon

On peut calculer cet horizon pour un rayon reçu (horizon du passé) ou émis (horizon du futur). La forme de Lancros est symétrique par rapport à τ= 0.

a)         Considérons un observateur à τ = 0 et ψ =0. Du fait de la symétrie, les distances d’horizons du passé et du futur seront égales dans ce cas.

Ce ne sera pas le cas pour un observateur quelconque (on illustrera brièvement ce cas).

Calculons le temps mis par un rayon lumineux émis radialement au temps t_e, à une distance angulaire ψ _H d’un observateur, vers cet observateur (situé à ψ =0) et reçu par lui à τ =0.

ds²= -dτ² + cosh²τ.dψ² =0 , → dτ²/cosh²τ = dψ²,→ dτ/coshτ  =±dψ.

On va s’intéresser à la propagation vers les ψ croissants (dψ/ dτ>0): dτ/coshτ  =+dψ

Il faut intégrer[18] le long du chemin de ψ  = ψ _H  à  ψ = 0, (τ=t_e à τ =0).

∫ _te⁰ dτ / coshτ  = [2arctg (exp(τ))] _te⁰ =∫ _{ψ H} ⁰  dψ = – ψ _H 

Si t_e,→ -∞, ce qui correspond l’horizon du passé des évènements, on obtient:

[2arctg (exp(τ))]-∞⁰ = 2arctg (exp(0)) – 2arctg (exp(-∞)) = 2.π/4 – 0 = π/2 = -ψ _H 

Dans l’autre sens (horizon du futur) on aurait eu ψ _H  = π/2.

Cette valeur de ψ _H  = π/2 correspond bien à celle de la singularité de la forme (1.3)

• Si l’observateur est quelconque ψ  = ψ _r et (τ=t_r)

∫ _te^tr dτ / coshτ  = [2arctg (exp(τ))] _te^tr =∫ _{ψ H} ^{ψ r}  dψ = ψ _r – ψ _H

Si t_e,→ -∞, ce qui correspond l’horizon du passé des évènements,

ψ _H = ψ _r – 2arctg (exp(tr))

On voit que ψ _r – ψ _H  ne dépend que de t_r. (Classes d’observateurs)

On pourrait calculer l’horizon du futur par la même méthode: observateur de coordonnées  ψ = ψ _e et (τ=t_e)

∫ _te^tr dτ / coshτ  = [2arctg (exp(τ))] _te^tr =∫ _{ψ e} ^{ψ H}  dψ = ψ _H – ψ _e

Si t_r,→ ∞, ce qui correspond l’horizon du futur des évènements, 

ψ _H – ψ _e  = 2arctg (exp(∞)) – 2arctg (exp(t_e)) = π/2 – [2arctg (exp(t_e))]

On voit que pour t_e ,→ ∞, 2arctg (exp(t_e)) → π/2→ ψ _H – ψ _e  → π/2 – π/2 → 0

Ce qui était intuitivement prévisible, compte tenu de l’expansion « exponentielle » quand t → ∞, celle-ci croît si rapidement que l’horizon des évènements pour chaque observateur tend vers zéro. L’univers devient totalement causalement déconnecté.

—————————————————————————————————————–

Cela éclaire la nature de la singularité notée par Weyl. Dans cette forme, on ne peut pas parler « d’annulation » de la vitesse de lumière localement sur cet « horizon ».

Simplement l’expansion fait que pour cette distance (entre l’observateur et l’horizon associé), l’accroissement « spatial » de la géodésique par intervalle de temps dt vaut c.dt (autrement dit pendant que le photon juste émis parcourt c.dt, du fait de l’accroissement de c.dt de la géodésique, la distance à parcourir reste la même, le photon fait du surplace vis-à-vis de l’observateur distant, il ne l’atteindra jamais).

On voit que cela s’évalue par une intégrale sur le chemin à parcourir.

Ce qui fait qu’au-delà de cet horizon aucun signal vers l’observateur ne peut l’atteindre, (c’est un horizon des évènements) mais cela n’est pas une vraie singularité, des géodésiques le traversent dans les deux sens : cet horizon est propre à cet observateur.

En effet à la différence d’un horizon comme celui de la solution de Schwarzschild qui est le même pour tous les observateurs extérieurs, celui est propre à chaque observateur.

Cette forme montre la vraie nature de cette singularité qui n’est autre que la limite de l’univers observable pour un observateur donné.

Formes avec section spatiale ouverte

Il existe une forme avec k = -1 dans les équations de Friedmann-Lemaître : elle s’écrit :

ds²= -dτ² + sinh²τ (dψ² + sinh²ψ (dθ² + sin²θ.dφ²))

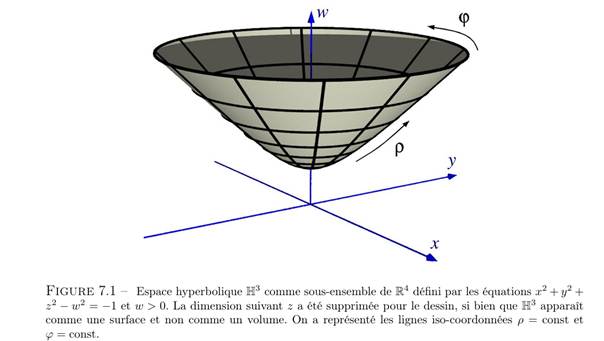
Dans cette forme, les sections spatiales sont de type hyperbolique (H³).

La forme décrit toute la variété (extension analytique maximale)

Forme de Lemaître[19] (1925)- Robertson(1928)

Lemaître n’appréciait pas la forme originale (1) car elle semblait privilégier un centre fixe[20],  alors qu’elle était manifestement spatialement homogène.

Il a cherché, indépendamment des travaux de Lancros dont il n’a pas eu connaissance, une expression qui reflétait la symétrie de la solution, il a proposé[21]:

ds² = -dt² + exp(2t/R).(dr² + r²(dθ² + sin²θ.dφ²))                                                   (3.1)

a) Il n’y a pas de singularité apparente, mais un calcul similaire au précédent montre qu’il a un horizon des évènements à r = R, ce qui correspond à la singularité de la forme (1.2)

b) Notons que la forme (3.1) est également non statique (dépend du temps propre).

c) Les observateurs « comobiles » sont en chute libre:  la coordonnée t est le temps propre.

d) La solution est spatialement ouverte (exp(2t/R) → ∞ quand t→  + ∞ ).

e) Les sections spatiales (t = cste) sont « euclidiennes » à la différence de la forme de Lancros.

f) En fait c’est la métrique de Robertson Walker pour k =0 et a²(t) = exp(2t/R)[22].

• La solution ne décrit pas toute la variété, à la différence de celle donnée par Lancros[23].

————————————————————————————————————–

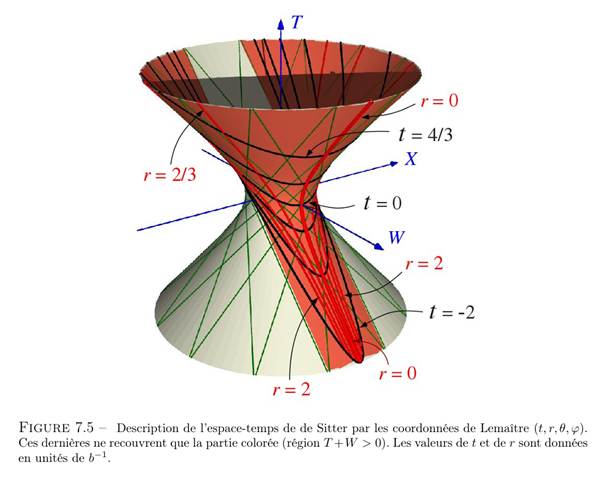
Calcul du rayon de l’horizon

C’est le même type de calcul que précédemment.

Cette forme ne possède pas la symétrie de celle de Lancros.

Faisons le calcul pour un observateur particulier r = 0 et t = 0.

Calculons le temps mis par un rayon lumineux émis radialement au temps t = 0 par un observateur situé à r = 0, et reçu à t_r à une distance r_H  de cet observateur.

ds²= dt² – exp(2t/R).dr² =0  → dt²/exp(2t/R) = dr²→  dt. exp(-t/R) =dr,

Il faut intégrer le long du chemin de r = r _H  à r = 0, (t = t_e à t =0).

∫ ₀^tr dt.exp(-t/R) = – [R.exp(-t/R)] ₀^tr =∫ ₀^rH dr, = r _H 

Si t_r → ∞, ce qui correspond à un horizon des évènements, on obtient :  r _H  = R

Cette valeur de r _H correspond bien à celle de la singularité de la forme (1.2)

Il est facile de vérifier que ce calcul s’adapte facilement au cas général.

Pour un temps infini, cet horizon se réduit à zéro comme dans le cas de la forme de Lancros.

Commentaires sur la diversité des formes

Toutes ces formes décrivent le même espace-temps, mais dans des coordonnées différentes.

La diversité de géométrie et de topologie des sections spatiales de ses formes, décrivant le même espace-temps, montre que c’est l’espace-temps qui a une réalité physique et pas on feuilletage en temps et espace. Il ne faut donc pas trop s’en préoccuper pour en déduire des caractéristiques physiques

L’espace-temps de « De Sitter » est-il vraiment une solution des équations d’Einstein ?

Dans le chapitre précédent nous n’avons utilisé que des critères généraux géométriques sur les variétés, sans faire intervenir à quelque moment que ce soit la Relativité Générale.

Nous avons trouvé une solution où les contraintes liées à la symétrie déterminent la forme métrique de cet espace-temps (le seul paramètre libre est la valeur de la courbure : elle définit complètement la variété).

Comme à aucun moment nous n’avons utilisé la Relativité générale pour établir la solution complète correspondant à l’univers « De Sitter », nous pouvons déclarer que l’Univers de « De Sitter » n’est pas une solution de la Relativité Générale.

L’équation d’Einstein avec constante cosmologique Λ dans le vide (De Sitter) s’écrit :

R_μν – ½ g_μν (R -2Λ) = 0                                                                    (5-1)

En élevant un indice et en contractant on obtient :

R – 2R + 4 Λ = 0 → R = 4 Λ

(4-2) nous donne la courbure normalisée :

K = R/n(n-1) = R/4.3 = R/12 = Λ/3

Cette solution satisfait l’équation d’Einstein car le tenseur d’Einstein a été construit à partir du tenseur de Ricci, du scalaire de Ricci et la métrique, pour obtenir un tenseur de divergence covariante nulle.

Si dans cette construction, on ajoute une constante au scalaire de Ricci, par exemple, la divergence du nouveau tenseur ainsi construit va satisfaire également à la condition de divergence nulle. Nous avons toute une classe de « tenseurs d’Einstein » potentiellement valides pour son équation, correspondant à une classe d’univers (différentiés entre autres par la condition de courbure à la limite lorsque la densité de matière → 0).

Elle permet de relier la constante cosmologique au scalaire de Ricci, dans le cadre de cette équation, mais notons que cette information ne nous a absolument pas servi dans l’établissement de la solution (seul le signe de la courbure a été utilisé).

Si la constante cosmologique avait un sens physique[24] l’équation d’Einstein apporterait quelque chose en reliant un paramètre géométrique (la courbure) à un paramètre physique, mais ce n’est pas le cas.  L’équation d’Einstein n’a donc pas de valeur ajoutée sur cet aspect.

Rappelons qu’en Relativité générale, pour chercher une solution, nous devons utiliser une métrique « générique» à priori dont on spécifie la forme à partir d’un certain nombre de considérations géométriques à priori sur une Variété « générique » dont on induit qu’elle va servir de trame à notre solution, et qu’on applique l’équation d’Einstein pour contraindre (par la matière énergie) ces éléments génériques pour obtenir si possible une solution complètement définie.

Cette contrainte ne porte que sur la trace du tenseur de Riemann, (pas sur le tenseur de Weyl)  trace qui est nulle en cas de solution dans le vide.

On peut donc se demander si une solution dans le vide est une solution de la Relativité Générale, ou si elle est simplement une solution géométrique, exprimée dans le formalisme de la Relativité Générale (La matière n’apporte aucune contrainte à la partie géométrique de l’équation, qui est complètement définie par la métrique).

On remarque par exemple, que des travaux comme la classification de Petrov qui s’appuient sur le tenseur de Weyl, le font sur des considérations purement géométriques qui n’ont rien à voir avec la Relativité Générale. Il convient donc d’être attentif aux apports respectifs.

L’indépendance de la solution De Sitter vis-à-vis de la Relativité générale sauve t’elle le principe de Mach ?

Einstein prétend qu’une solution d’espace-temps ne saurait exister sans matière.  Cette matière détermine le tenseur métrique g_μν et crée l’inertie. Ici c’est la symétrie de la solution qui détermine la métrique, sans recours à l’équation d’Einstein, cela ne plaide t’il pas en faveur d’une non contradiction de la Relativité Générale avec le principe de Mach ?

Cela ne résout pas tout, car des solutions comme celle de Schwarzschild posent également un sérieux problème. Une masse unique peut elle avoir une inertie ?

La solution de Schwarzschild ne répond pas à cette question, le paramètre de masse qu’on calcule pour la singularité centrale ne correspond pas à une masse inerte, mais à une masse gravitationnelle active qui se calcule d’ailleurs à partir de critères géométriques (Intégrale de Komar). Là encore il y a matière à réflexion sur la compatibilité avec le principe de Mach dans cette solution. Elle génèrerait l’inertie pour les autres masses, (encore que le problème du mouvement de particules dans un champ soit un problème complexe) mais l’histoire ne dit pas si elle en a une.

Energie du vide et inertie

Quand on considère les différents types d’espace-temps en Cosmologie Relativiste et les équations de Friedmann Lemaître, on déduit une relation importante (conservation covariante de l’énergie):

d(ρ.a³)/dt = – p.d(a³)/dt          →        dU + P.dV =0             (7-1)

où ρ est la densité d’énergie et a(t) le facteur d’échelle dépendant de t.

En interprétant de façon thermodynamique cette relation, elle exprime la relation entre la variation d’énergie contenue dans un volume comobile U = ρ.a³  (membre de gauche) et le travail fourni (membre de droite) P.dV= p.d(a³).

Pour l’énergie du vide (constante cosmologique) le fluide est à densité constante ρ_v et de pression p_v = – ρ_v. L’équation (7-1) s’écrit : dU + P.dV ≡ 0.

Ceci fait dire que l’énergie du vide n’a pas d’inertie (pas de masse inerte).

L’univers de « De Sitter » est-il statique ou dynamique ?

Il semble difficile de donner un sens physique à cette question, puisque pour une même solution, comme nous l’avons vu, cela dépend de la forme de la métrique qu’on utilise : Certaines sont statiques d’autres dynamiques.

Rappelons qu’on peut décrire synthétiquement la variété sans avoir à privilégier une quelconque des coordonnées par sa courbure (4D) qui est constante partout dans la variété du fait de l’homogénéité de la solution.

De toute façon les coordonnées, ne sont que des étiquettes pour repérer les points de la variété qui inclut l’espace et le temps et du fait de la covariance il n’y a aucune raison de privilégier une de ses coordonnées individuellement.

Que dans une forme de la métrique, la partie spatiale dépende du temps ou l’inverse n’est finalement qu’un problème géométrique d’agencement interne.

Que définit vraiment la Relativité Générale ?

Les géodésiques, par exemple, ne sont-elles que des courbes géométriques qui traduisent simplement une propriété géométrique (transport parallèle du vecteur tangent). La géodésique définie comme extremum local d’une courbe utilise une métrique et l’équivalence des deux concepts[25] se fait à travers l’identification des coefficients de connexion affines et métriques.

Les particules de test qu’on introduit pour tracer la dynamique interne, font elles partie de la théorie ou sont-elles un ajout, nécessité par le souci de faire de la physique ?

Pour les univers non vides l’équation d’Einstein, par la présence du tenseur énergie impulsion, munit la solution d’un caractère physique et le problème de sa dynamique a un sens physique.

En particulier le référentiel chute libre est matérialisé[26] et déterminé par la matière énergie ce qui donne un sens physique au mouvement de particules de test par rapport au référentiel.

L’équation du mouvement (T^μν_{; ν} = 0) se déduit du tenseur  énergie impulsion d’un fluide.

Pour les univers vides, les « particules de test » matérialisant les géodésiques, ont-elles une motivation physique, alors qu’aucun élément physique n’intervient dans la construction de la solution[27] ?

A priori les géodésiques nulles sont plus appropriées pour décrire ces espaces

Le temps propre (grandeur à 4 dimensions à qui on peut attribuer un caractère physique : on sait le mesurer) est un paramètre affine privilégié pour baliser les géodésiques temporelles physiques.  Cette propriété ne structure-t-elle pas la forme de la métrique, en privilégiant celle où la variable temps est le temps propre (Observateurs en chute libre)[28]. 

La Relativité Générale est assez ambiguë là-dessus, d’autant qu’on sait que les « bonnes » variables ne peuvent être que globales, du fait de l’invariance par difféomorphisme. Son utilisation pour faire de la physique échappe t-elle à une interprétation de la théorie ?

Et alors quid des autres types de géodésiques et des lignes d’univers non géodésiques[29]?

On voit que souvent (mais pas toujours) on est plus à l’aise avec une forme où la coordonnée temps est le temps propre des observateurs associés à cette forme. Mais n’est-ce pas que simple commodité ou habitude issue des méthodes classiques. La Relativité Générale clamant haut et fort que tous les référentiels se valent, nous incite à ne pas tirer de conclusions générales d’éléments spécifiques à cette approche, avant d’en avoir vérifié la portée.

9 Conclusion sur l’espace-temps de De Sitter

Nous avons vu que l’horizon de la solution de l’univers de De Sitter était fictif. Par ailleurs nous avons discuté du caractère relativiste de cette solution et montré que cela n’était pas si évident que cela.

Chapitre 3 : Espace-temps anti-De Sitter^[30]

Etablissement de la métrique

Comme pour l’espace-temps de De Sitter, définissons une variété fictive plate à 5 dimensions de métrique :

ds₅ = -u²-v² °x²+y²+z²

et imbriquons un hyperboloïde défini par :

-u² -v² +x²+y²+z² = -α²                       (1)

Remarquons les 3 signes négatifs.

Nous allons définir des coordonnées {t’, ρ, θ, φ} sur l’hyperboloïde par :

u = α sin(t’) cosh(ρ)

v = α cos(t’) cosh(ρ)

x = α sinh(ρ) cos(θ)

y = α sinh(ρ) sin(θ).cos(φ)

x = α sinh(ρ) sin(θ).sin(φ)                                                                 (2)

qui définissent une métrique sur l’hyperboloïde de la forme :

ds² = α²(-cosh²(ρ)dt’²+dρ² + sinh²(ρ)dΩ₂²)                                        (3)

Notons que t’est périodique, ce qui n’est pas trivial. Selon (2) on voit que t’ et t’ + 2π définissent le même endroit sur l’hyperboloïde. Comme ∂_t’ est de type temps partout, une courbe à coordonnées {ρ, θ, φ} constantes, lorsque que t’ va croître, va être une courbe fermée. [31]

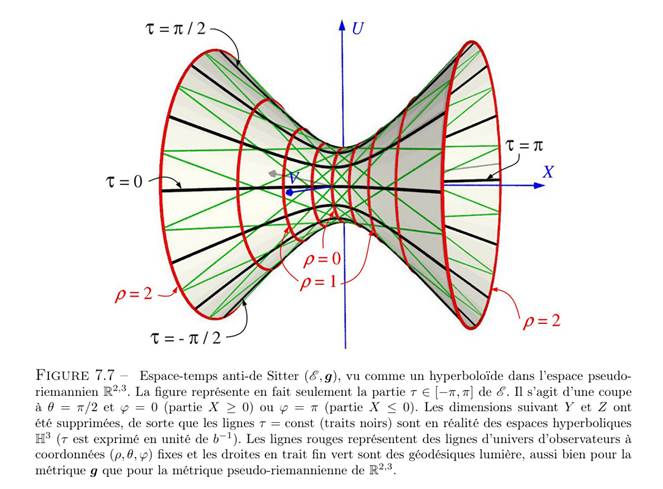
Cependant, ce n’est pas une propriété intrinsèque de cet espace-temps mais un artefact de la manière dont nous avons dérivé la métrique d’une imbrication particulière.

Il est souhaitable de considérer cet espace-temps de recouvrement de cette variété avec la métrique définie en (3) qui permet de faire varier t’ de -∞ à + ∞ où il n’y a pas de courbes fermées dans cet espace-temps que nous définirons comme l’espace-temps anti-De Sitter.

Diagramme conforme de la métrique

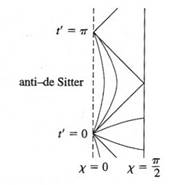
Figure 1. Diagramme conforme de l’espace-temps anti De Sitter. Les sections d’espace ont la topologie de R², que nous avons représenté en coordonnées polaires, ce qui fait que les points du diagramme représentent des 2-sphères excepté pour le bord gauche où ce sont des points à l’origine de l’espace. L’infini, à droite, est une surface de type temps.

Contrairement à De Sitter, la coordonnée radiale apparaît dans le facteur conforme. De plus, pour anti-De Sitter, la coordonnée t’ varie de moins l’infini à plus l’infini, tandis que la plage de la coordonnée radiale vaut :

Donc, anti-de Sitter est en relation avec la moitié de l’univers statique d’Einstein.

Le diagramme est représenté sur la figure 1, qui illustre quelques géodésiques de type temps et espace représentatives passant par le point t’ = 0, χ = 0. Comme χ varie seulement de 0 jusqu’à π/2, au lieu de π, une section spatiale de cet espace-temps a la topologie de l’intérieur d’un hémisphère de S³ ; c.a.d, est de topologie R³ (et l’espace-temps complet a donc la topologie R⁴).

Notons que nous avons représenté le diagramme en coordonnées polaires, tel qu’un point à gauche représente un point à l’origine spatiale, tandis qu’un sur la droite représente une 2-sphère à l’infini spatial.

Propriétés originales de l’espace-temps AdS

Une propriété intéressante d’anti-de-Sitter est que l’infini est une hypersurface de type temps définie par χ = π/2. Comme l’infini est de type temps, l’espace n’est pas globalement hyperbolique, ce qui ne correspond pas à un problème, avec une valeur initiale, bien posé en termes d’information spécifié sur la section spatiale, du fait que de l’information, venant de l’infini, peut toujours entrer. Une autre propriété intéressante est que la carte exponentielle n’est pas sur l’espace-temps global, des géodésiques telles que celles dessinées sur la figure 1, qui sont issues d’un certain point ne couvrent pas toute la variété.

Les géodésiques de type temps, orientées vers le futur, peuvent initialement se poursuivre radialement vers l’extérieur, de t’ = 0, χ = 0, mais éventuellement se refocaliser au point t’ = π,  χ = 0 et vont donc se poursuivre radialement vers l’extérieur à nouveau.

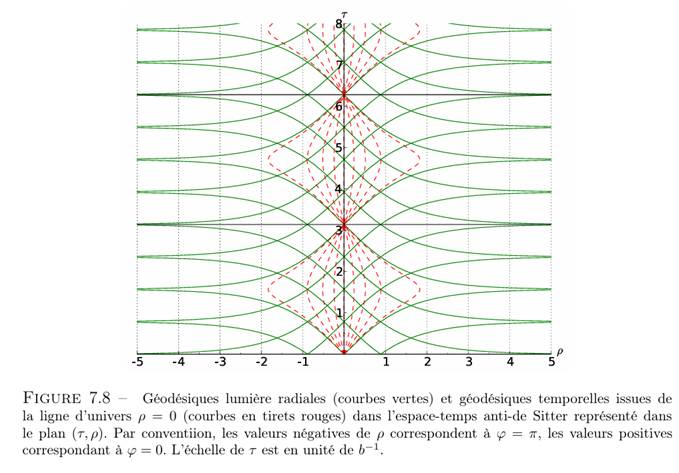
Ce diagramme, dans ces coordonnées, montrent comment un observateur (ici celui dont la ligne d’univers est la droite verticale au centre, sort du cône de lumière, qui s’évase asymptotique parallèle à une droite horizontale à  tau = π/2, pour tau > π/2.

Sortant du cône de lumière, la causalité par rapport à des conditions initiales définies au sommet du cône,  la situation devient imprédictible.

Correspondance ADS/CFT

Accessoirement, on ne peut s’empêcher de souligner que la nature de type temps de l’infini induit une propriété remarquable de la théorie des cordes, la correspondance AdS/CFT. AdS est l’espace-temps anti-de-Sitter que nous avons présenté et CFT désigne les  théories des champs conformément invariantes définies sur le frontière qui, pour un AdS de dimension n, est un espace-temps de dimension (n -1) sur sa frontière  à droite.

La correspondance AdS/CFT suggère que, dans une certaine limite, il y a équivalence entre une théorie de gravité quantique (ou d’une version supersymétrique d’elle) entre un fond AdS et une théorie des champs, conformément invariante, non gravitationnelle, définie sur la frontière.

Comme nous avons bien plus de connaissances sur les théories quantiques de champs non gravitationnelles que nous en avons sur les théories quantiques gravitationnelles, cette correspondance (si elle s’avère vérifiée ce qui est probable, mais non démontré) serait d’une grande utilité pour ouvrir une voie vers une théorie quantique de la gravitation.

Voir : http://ncp.edu.pk/docs/snwm/pervez_hoodbhoy_001_ads-space_introductory_moschella.pdf

Pour complément d’information.

Références :

Bronstein I.N & Semandiaev K.A (1982),  Eléments d’analyse mathématiques, In « Aide mémoire de mathématiques », 7ème édition (formule 433) p 570  (Eyrolles)

Carroll S. M (2004). Spacetime and Geometry. Pearson-Addison Wesley. Maximally symmetric universes p323-329

De Sitter. W. (1917a). “On the relativity of inertia. Remarks Concerning Einstein ‘s latest hypothesis”. Koninklijke Akademie van Wetenschappen te Amsterdam. Section of Sciences. Proceedings 19:1217-1225

De Sitter. W. (1917b). ”On the curvature of space”. Koninklijke Akademie van Wetenschappen te Amsterdam. Section of Sciences. Proceedings 20:229-242

De Sitter. W. (1918). “Further remarks on the solutions of the field Equations of Einstein Theory of gravitation”. Koninklijke Akademie van Wetenschappen te Amsterdam. Section of Sciences. Proceedings 20:1309-1312

Earman J. & Eisenstaedt J.(1999). Einstein  and Singularities. Stud.Hist.Mod.Phys. Vol 30.N°2 pp185-235. Elsevier Science Ltd GB

Eisenstaedt J.(1993) « Lemaître and the Schwarzschild Solution. » In New Studies in the History of General Relativity. Proceedings of the Third International Conference on the History and Philosophy of General Relativity.Einstein Studies, Vol. 5, John Earman, Michel Janssen, and John D. Norton, eds. Boston: Birkhäuser,

Eisenstaedt J. (2003). Einstein et la relativité générale, les chemins de l’espace-temps. P 254.

Gourgoulhon E. Cours de Relativité Générale IAP (2013-2014) chapitre 7 p.167-201 (figures 7-1, à 7-8)

Klein F.(1918a). “Bemerkungen über die Beziehungen des De Sitterschen Koordinatensystem B zu der allgemeinen Welt konstanter positiver Krümmung“. Koninklijke Akademie van Wetenschappen te Amsterdam. Section of Sciences. Proceedings 21(1918-1919): 614-615

Klein F.(1918b). “Über die Integralform der Erhaltungssatze und die Theorie der raümlichgeschlossenen Welt“. Königliche Gesellschaft der Wissenschaften zu Göttingen. Nachrichten: 394-423

Lancros C. (1922a). «Ein vereinfachendes Koordinatensystem für die Einsteinschen  Gravitationsgleighlungen». Physikalische Zeitschrift 23: 537-539

Lancros C. (1922b). «Bemerkung zur De Sitterschen Welt». Physikalische Zeitschrift 23: 539-543

Lemaître G. (1925a) “Note on De Sitter’s Universe.” Publication du Laboratoire d’Astronomie et de Géosésie de l’Université de Louvain 2 :37-41. & Journal of Mathematics and Physics 4 : 188-192

Lemaître G.(1925b). »Note on De Sitter’s Universe ». Phys. Rev. 25 :903

Szekeres G. (1960). On the singularities of a Riemannien manifold. Publ. Mat. Debrecen  7, 285-301.

Weyl H.(1919)”Über die statischen Kugelsymmetrischen Lösungen von Einsteins kosmologischen Gravitationgleichungen” Physikalischer Zeitschrift 20: 31-34

---

[1] Ce document reprend des éléments du livre « Spacetime and geometry de S. Carroll (Addison Wesley) » à consulter pour plus de détails, et en développe certains éléments.

[2] Pour ces symétries on utilise la version du tenseur de Riemann avec tous les indices bas qu’on obtient en abaissant un indice sur la définition que nous avons donnée dans les rappels par multiplication par le tenseur métrique et contraction pour éliminer l’indice haut. En fait, on montre ces propriétés sur sa valeur exprimée en coordonnées localement inertielles. Dans cette version, il est évident qu’il est antisymétrique sur ses 2 premiers et 2 derniers indices, invariant par échange de la première paire avec la seconde la somme des permutations sur les 3 derniers indices est nulle, ceci fait que sur les 256 composantes il n’y a, au maximum, que 1/12 (n²(n²-1)) valeurs différentes, soit 20 pour n = 4. Il peut y en avoir moins si des contraintes s’appliquent (symétries).

[3] Adapté de Carroll S. M (2004). Spacetime and Geometry. Pearson-Addison Wesley. Maximally symmetric universes p139-141 & p323-329.

[4]Nous ne traitons pas ici de l’autre solution à symétrie maximum, celle à courbure négative constante, l’espace anti-Sitter. Notons que cet espace Anti De Sitter sert « d’espace de fond » dans certaines cosmologies branaires.

[5] Il conviendrait de faire la différence entre courbure intrinsèque et courbure extrinsèque. Le choix à priori de l’hypersurface « Hyperboloïde » imbriqué dans un espace Minkowskien 5D, s’appuie sans doute sur la connaissance de la courbure d’une telle hypersurface compatible avec ce qu’on recherche.

[6] On ne le redémontre pas, mais c’est la même intégrale que pour la forme (2.1). Scalaire de Ricci = 12/α²

[7] Remarque sur les notations : Par 2-sphère nous entendons la surface (à deux dimensions) d’une sphère classique, par une 3- sphère il s’agit d’une hypersphère 3D.

[8] On pose c =1,  on adopte la signature (-+++), par matière c’est au sens matière énergie, dans le document.

[9] Forme originale donnée par De Sitter: Cité dans Earman J. & Eisenstaedt J. (1999) p 192. Scalaire Ricci =12/R²

[10] Ce point est exposé en détail dans : Earman J. & Eisenstaedt J. (1999)

[11] Cité dans Eisenstaedt (1993) p. 357

[12] Weyl (1919) p. 31

[13] Citée dans Szekeres (1960) p285, le scalaire de Ricci vaut 12/R², il est constant (Mathematica 4)

[14] De Sitter (1917b p.230) a également proposé cette forme. Cité dans Eisenstaedt  (1993) p.355

[15] Lancros(1922a) et Lancros (1922b)

[16],Cité dans : Eisenstaedt J. (1993) Lemaître and the Schwarzschild solution, The Attraction of Gravitation : New Studies in the History of General Relativity. J. Earman, M. Janssen, J.D. Norton editors p 358

[17] Klein (1918a, 1918b)

[18] Bronstein I.N & Semandiaev K.A (1982), donne l’intégrale de ∫dx/cosh (ax) = (2/a)arctg[exp(ax)], p 570

[19] Lemaître (1925), établie indépendamment par Robertson (1928) cité : Earman J. & Eisenstaedt J.(1999) p202

[20] Notons que Lemaître s’attache à l’homogénéité spatiale (pas à l’homogénéité totale).

[21] Robertson a proposé la transformation suivante : r’=r.exp(-t/R), t’=t– (R/2)ln(1-r²/R²). Dans (5), r’→r, t’→t.

[22] On peut l’obtenir comme solution du vide de l’équation de Friedman Lemaître (avec constante cosmologique)

[23] La transformation de Robertson montre qu’on ne peut pas étendre indéfiniment vers le passé les géodésiques temporelles. Cité dans Earman J. & Eisenstaedt J.(1999) p202

[24] Il y a des hypothèses: énergie du vide, quintessence, par exemple, mais aucune n’a donné satisfaction aujourd’hui, les tests cosmologiques semblent toutefois privilégier l’hypothèse d’une «constante cosmologique».

[25] Gourgoulhon.E Cours de Relativité Générale IAP (2006) p.82-86

[26] Le Rayonnement de Fond Cosmologique (RFC) dans la solution Friedman Lemaître Robertson Walker

[27] On parle ici de particules de test virtuelles, dans le cas de particules matérielles «réelles », c’est plus complexe. Earman  J. & Eisenstaedt J. (1999) chap. 7 « The problem of motion » p 204-224

[28] Dans certaines solutions dans le vide, les formes les plus utilisées ne sont pas celles là (Schwarzschild, Kerr,..)

[29] A moins que la RG ne considère que des géodésiques, les mouvements non géodésiques, n’en feraient pas partie. Par exemple pour une fusée ce serait le centre de masse qui serait concerné par la RG…

[30] Traduction des pages 326-328 de « Spacetime and geometry » de S. Carroll, édition.Addison-Wesley. Se reporter à l’ouvrage en cas de doute.

[31] Les figures 7-1 à 7-8 sont extraites du cours de relativité Générale de Eric Gourgoulhon. https://luth.obspm.fr/~luthier/gourgoulhon/fr/master/relatM2.pdf