L’espace-temps seul a une nature physique en relativité
Comme, seul, l’espace-temps a une nature physique en relativité, le temps et l’espace étant réduits à en être que des « ombres » comme Minkowski l’a déclaré en 1907, on peut se demander si cette question présente vraiment un intérêt.
La différence entre espace et temps a une nature « relationnelle »
Rappelons d’abord, que comme l’espace et le temps ne sont que des caractères (des ombres) de l’espace-temps les relations entre l’espace et le temps ne sont que des relations entre ces « ombres » de cet espace-temps.
L’intérêt est que comme, physiquement nous ne mesurons, en général, que des « ombres » des entités spatio-temporelles, (nous mesurerons des temps, des intervalles de temps, des positions dans l’espace ainsi que des intervalles d’espace), ces relations peuvent nous renseigner sur l’entité spatio-temporelle qui les produit. [1] C’est dans cet objectif que cette analyse peut être utile.
Des coordonnées d’espace et de temps sont utilisées dans la plupart (mais pas toutes) des formulations du « ds² », intervalle d’espace-temps. représentant sa métrique [2]
Dans le cas le plus simple, relativité restreinte, ce ds² s’écrit:
ds² =-c²dt² + dx²+dy²+dz²
qui fait intervenir, les coordonnées x, y, z pour l’espace et i.c.t pour le temps.
où « i » est le nombre imaginaire défini par racine carrée de -1.
Le tenseur métrique (Minkowski) représenté sous forme d’un tableau est:
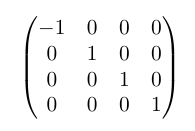
Cette métrique permet de définir des intervalles d’espace-temps de tous types (temps pour la matière, nul pour le rayonnement, espace).
Comme on peut tout aussi bien écrire
ds² =c²dt² – dx²-dy²-dz²
On voit que le caractère « imaginaire » d’une coordonnée traduit une propriété de type ‘ »relationnel » entre l’espace et le temps qui caractérise leur différence : L’espace n’est pas du temps et vice-versa.
Cette différence a-t-elle aussi une nature substantielle?
Dans le ds² on voit, dans la signature de la métrique (-+++) ou (+—) que espace et temps ont une action « opposée » sur la valeur du ds², comme leur signe opposé dans la formule le montre. C’est la conséquence de leur différence relationnelle. Comme une action a un caractère physique, ceci peut-il être considéré comme révélateur d’une différence substantielle?
En suivant Leibnitz qui caractérise l’existence par le fait qu’elle doit agir pour avoir un caractère physique, on est tenté de répondre oui.
Coordonnées de type nul
Ces coordonnées sont de nature espace-temps nativement.
Dans ces conditions, en appellant u, v, w, w*, où w et w* sont des nombres complexes conjugués,[3] dans ces coordonnées le ds² s’écrit:
ds² = -2du.dv +2dw.dw*
Le tenseur métrique, représenté sous forme de tableau est:

La signature de la métrique est (0,0,0,0) qu’on pourrait (en théorie) réduire à (0,0,0*). Trois coordonnées nulles (0) dont une complexe (0*), nativement, d’espace-temps suffisent à définir la métrique en relativité ce qui indique qu’elle n’a, nativement, que 3 degrés de liberté.
Ces coordonnées permettent également de définir tous les types d’espace-temps (de type temps, nul, espace). On peut se demander si avec ,seulement ,3 coordonnées nulles « réelles », signature (000), on pourrait définir totalement l’espace-temps « optique » ne comportant que des géodésiques nulles.
Nous avons évoqué les coordonnées, il faut rappeler que ces coordonnées s’appliquent sur une base de vecteurs linéairement indépendants.
Une difficulté réside dans le fait que l’utilisation de coordonnées nulles et d’une base de vecteurs nuls est moins familière à nos esprit que des coordonnées temps et espace et une base de vecteurs de « Minkowski ».
Voir « Penrose-Newmann formalism :Special relativity in null coordinates » pour plus d’information.
Notes
[1] Nous sommes dans la position des « prisonniers » de l’allégorie de la caverne de Platon qui ne voient que des ombres de la « réalité extérieure » sur les parois de la caverne. On se demande s’ils peuvent concevoir que ce qu’ils perçoivent n’est pas la réalité mais des ombres de quelque chose de plus complexe et, si oui, comment ces ombres pourraient permettre d’atteindre ou d’approcher cette réalité.
Notons dans notre vision binoculaire, à partir de deux images (chaque image est plane : une ombre 2D sur notre rétine), notre cerveau élabore une image 3D, probablement pas totalement correcte mais qui augmente l’information portée par les 2 images.
Il est probable que, pour ce faire, notre cerveau utilise aussi des informations sur les relations entre l’image 3 D de ce type et des projections 2 D (sur la rétine de chacun de nos yeux) acquises par ailleurs, par l’expérience passée.
Cet exemple peut servir de paradigme pour tenter de reconstituer l’entité espace-temps à partir de nos perceptions et mesures d’espace et de temps.
[2] Rappelons que formellement ds² désigne le tenseur métrique à 2 indices « covariants ». L’exposant « 2 » ne représente pas un « carré ».
[3] Etant conjugués il ne sont pas indépendants, il n’y a donc que 3 degrés de libertés au lieu de 4. La nécessité de w et w* est imposée par la contrainte de permettre le changement de coordonnées vers des coordonnées de temps et d’espace conventionnels comme dans la représentation de Minkowski, ce qui permet de définir tous les types d’espace-temps: de type temps, espace ou nul.
Les cordonnées u, v, w, w* sont définies à partir de t, x, y, z et vice-versa.
Mais on peut considérer qu’on a que 3 coordonnées, dont une de type complexe. Rappelons que ces coordonnées u, v, w, w* sont portées par une base de vecteurs de base qui sont eux mêmes nuls (et dont 1 est complexe).
Il n’y a que 3 degrés de libertés dans la représentation, car, comme un vecteur nul est orthogonal à lui même, il n’y a que 3 vecteurs nuls différents linéairement indépendants.
Peut-on définir l’espace-temps, de manière opérationnelle, avec seulement 3 vecteurs nuls, sans recourir dans les opérations, à un vecteur complexe? Cela permettrait il de définir totalement l’espace temps ou seulement l’univers « optique » (les géodésiques nulles)?