Introduction
Posé comme un des 2 postulats de sa théorie de la relativité en 1905, par Einstein, une analyse ultérieure voir: Vitesse limite en relativité : Cette définition a-t-elle un sens ? 07/07/24 , montre que le principe de relativité lui-même invoque un invariant, dont il ne précise pas la valeur, qui structure la théorie.
Selon que cet invariant est nul, non nul mais fini, ou infini on obtient respectivement une dégénérescence, une théorie du type relativité restreinte dans ce cas, ou la théorie classique newtonienne.
La lumière n’est pas essentielle, elle est un marqueur
Si on s’attache à la géométrie de l’espace-temps de la relativité restreinte, (L’espace-temps décrit par Minkowski qui la représente) on constate que les géodésiques nulles jouent un rôle structurel en régissant la causalité et divisant l’espace-temps en différentes régions: celles de type espace sans causalité, celles de type temps avec le passé, le présent, le futur, la frontière étant donnée par le « cône de lumière », une hypersurface de type nul. On voit que la lumière, en tant que phénomène physique n’y figure pas.
On fait l’hypothèse que la lumière suit les géodésiques nulles et, à ce titre, en est un marqueur.
La vitesse de la lumière est constante dans tous les référentiels
En relativité restreinte en, 1905, on stipule que dans tous les référentiels « galiléens » (inertiels et différant par une vitesse relative constante) la vitesse de la lumière est constante (mais pas sa fréquence). Ceci est contraire à la loi d’addition des vitesses newtonienne.
Ceci suggère que la nature de la lumière est de type fréquentiel, ceci étant corroboré par la variation de sa fréquence au lieu de sa vitesse.
Compte tenu que dans le ds² = -c²dt² +dx²+dy²+dz² décrivant l’intervalle d’espace-temps, qu’on peut intégrer en s² = -c²t² + x²+y²+z² dans le cas de la relativité restreinte ne traitant que de référentiels galiléens, le signe du temps étant différent de celui de l’espace, on conçoit que la nature physique du temps soit représenté mathématiquement par un objet dual (une fréquence) d’une entité de type spatial continue, comme le permettent les transformations de Fourier.
Qu’appelle -t-on vitesse?
La vitesse de coordonnées
Ayant défini un repère, une base de n vecteurs orthonormés, dont n-1 de type espace et un de type temps, linéairement indépendants, on appelle vitesse v, comme dans la théorie classique, v= dl/dt où l² = x²+y²+z².
Appelons cela vitesse de coordonnées.
Mais t, x, y, z sont des coordonnées et alors que dans la théorie classique on pouvait accorder à ces coordonnées un caractère physique du fait de l’existence d’un espace et d’un temps (paramètre dynamique) universel, en relativité, cette vitesse est un indicateur qui n’a pas de caractère physique
La 4-vitesse, paramètre à caractère physique, permet des vitesses tendant vers l’infini.
Ce n’est pas le cas en relativité où on introduit le concept de 4-vitesse où, par exemple pour une ligne d’univers de type temps, le paramètre dynamique et affine (qui sert à mesurer la ligne d’univers) est ce qu’on appelle le « temps propre ».
Ce temps propre , mal nommé, et source de confusion avec la coordonnée temps, est en fait un paramètre de nature » intervalle d’espace-temps« , qui est proportionnel à cet intervalle d’espace-temps. On le trouve dans la métrique, avec un indice 2, et noté s² .
Ceci change tout, car alors qu’on a l’impression de ne pas pouvoir se déplacer dans un univers « plus vite que la lumière », si on prend le temps propre d’un observateur comme paramètre affine, ce qui est physiquement justifié, il pourrait traverser tout l’univers en une fraction de seconde, lorsqu’il s’approche de la vitesse « de coordonnée » de la lumière.
Comme c’est la 4-vitesse relativiste qui a un caractère physique, on voit que contrairement aux idées reçues, il n’y a pas (théoriquement) de vitesse physique limite.
Quid de la lumière?
La lumière parcourant des géodésiques de type nul, son « temps propre » est nul et avec ce paramètre un photon traverserait « instantanément » l’univers.
Pour s’affranchir de cela, considérant que du fait de la nature « fréquentielle » de la lumière, ce paramètre temps propre ne s’applique pas, on prend un autre paramètre affine pour les géodésiques nulles qui est sa « fréquence », en fait le 4-moment qui ne dépend que de sa fréquence.
Voir More about the Newmann-Penrose (NP) formalism 08/5/24
L’effet Doppler Relativiste décrit la possibilité d’une 4-vitesse infinie
Alors, tout devient clair. Dans un référentiel R1, animé d’une vitesse v, par rapport à un référentiel R0 , la lumière émise à une fréquence f1, liée à une transition entre couches électroniques, propre à un atome déterminé, identifiée par ses motifs de raies spectrales comme on l’utilise en spectrométrie, est observée à une fréquence f0 dans R0, différente décalée (l’effet Doppler relativiste fait intervenir le « facteur de Lorentz » ce qui montre que ce rapport tend vers l’infini quand la vitesse v tend vers la vitesse de la lumière).
L’observateur de R0 peut évaluer cette 4-vitesse de R1 par cette formule. [1]
L’énergie pour obtenir cette vitesse infinie
Nous savons que l’énergie est la grandeur physique associée au temps. Un calcul simple montrerait que pour faire tendre la vitesse d’un observateur vers la vitesse de la lumière, l’énergie qu’il va acquérir va tendre vers l’infini. Cela nous amène à réfléchir à la place de l’énergie dans la théorie.
à suivre
Notes
[1] Selon que le signal lumineux de fréquence f1 dans R1 est émis vers l’observateur de R0 ou en sens contraire le décalage est vers le bleu ou vers le rouge (la formule de l’effet Doppler relativiste inclut un vecteur de propagation).
De plus la situation est symétrique ce qui est dit pour R1 dans R0 est aussi vrai pour R0 dans R1.
[2] Formule de l’effet Doppler relativiste dans le cas le plus général (Wikipedia)

vs est la vitesse du référentiel qui émet le rayon lumineux, v0 est la vitesse du référentiel dans lequel elle est mesurée, et thétas sont les angles entre la source lumineuse et le référentiel d’émission et l’angle que font les référentiels. Pour plus de précisions sur les autres notations, voir https://fr.wikipedia.org/wiki/Effet_Doppler_relativiste.
Elle se simplifie si on pose que la vitesse de l’observateur v0 = 0, (comme les vitesses sont relatives on peut le considérer « au repos », pour simplifier. Comme dans notre exemple les référentiels sont parallèles tous les angles valent 0, donc cos(0) = 1 . Par ailleurs on peut poser c =1. on obtient alors:
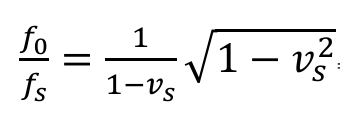
On voit que le facteur de Lorentz intervient dans la formule.