The collapse of a massive star into a black hole shows that while the star must « burn fuel », in this case fuses light chemical elements, which it has in limited quantities, to maintain the hydrostatic balance, where the expansion of the heated gas is compensated by the gravitational contraction, the gravitation, which does not seem to need anything at all, ends up overcoming this equilibrium when the star’s reserves are depleted.
For a massive star (more than 8 solar masses approximately), this occurs in spite, even of the quantum effects which, by the principle of exclusion of Pauli for the electrons then by the neutrons (more intense), can stop it and produce according to the mass of the star, white dwarfs and neutron stars.
That gravity seems to “need nothing”, in this process. As the nature, usually, does not provide “free lunch,”, is this a naive and Newtonian view of the problem?
While the pressure which results of the random motion of the atoms of the “gas” increases as the temperature increases, which is a classic thermodynamic representation, gravitation is represented by a spacetime which does not seem related, conceptually to that.
Although Einstein’s equation is a local equation, in relativity, the physical variables of gravity are global because they are associated with the global geometry of the universe.
This phenomenon depends on the type of space-time in which it occurs.
The case of the Schwarzschild solution
In a Schwarzschild-type solution, we know that the spacetime remains the same outside the initial surface of the star, the “gravitational flux” being preserved in a collapse with spherical symmetry, on the other hand it changes inside. of this surface where instead of matter there will be vacuum.
Schwarzschild’s space-time phenomenology
Schwarzschild’s metric suggests that space is static, this implying the problem of a singularity oo the horizon. We know, Paul Painlevé was the first in history (1921) to provide a metric which is not singular on the horizon, this implying to get rid of a static space. This solution and those of many others further show that the space is in eternal collapse as illustrated on the figure below.
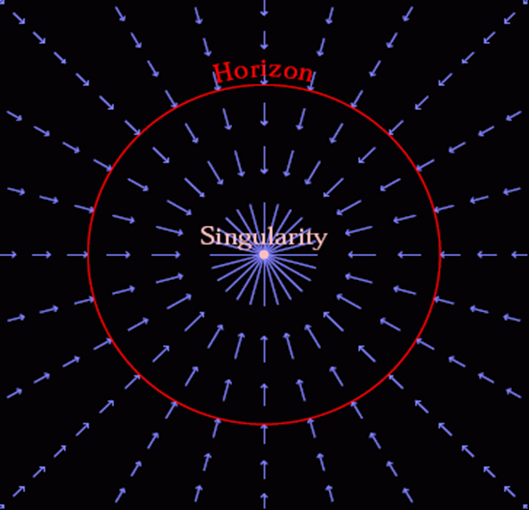
Therefore, the gas in the star is not static but outward going in this collapsing spacetime for maintaining its distance to the center of mass.
There is no mystery, it is because of the structure of this spacetime that free matter falls and would need energy for getting the acceleration requested for staying at the same distance of the center of mass. A static Schwarzschild observer is not a geodesic observer but an accelerated observer.
Last remark about white dwarfs and neutron stars where quantic effect (Pauli exclusion principle) looks to work permanently as gravitation does. Does this maintain an eternal the equilibrium ?
It would be interesting to understand this phenomenon.
What about quadrupolar gravitational waves?
The general rule is that a spherical collapse does not generate gravitational waves and that the lower order is provided by quadrupolar gravitational waves.