Rappel sur la dynamique, en gravitation

Ce qui intéresse le scientifique ce sont les lois du mouvement des corps en interaction gravitationnelle mutuelle: la dynamique d’un système. En effet c’est toujours à l’action d’un phénomène qu’on s’intéresse.

La mécanique newtonienne

Newton qui situait ces corps dans un espace euclidien tridimensionnel « absolu » (qui sert donc de référence), attribuait à chaque corps une masse active m_a, générant un « champ gravitationnel » s’étendant dans cet espace selon des lois qu’il précisait, une masse passive m_p, caractérisant le couplage de la masse avec le champ généré par les autres masses (mais pas par la sienne: pas d’auto-couplage). Il attribuait aussi une masse inertielle m_i, selon la célèbre loi f = m_i.a, où a est l’accélération que subit le corps, m_i, sa masse inertielle et f la « force » appliquée au corps.

Cette force f « invisible » s’exerçant à distance dans le vide, dérivait d’un potentiel scalaire (donc additif), ce qui permettait de calculer facilement le potentiel généré par des masses distantes en tout point. Connaissant, ce potentiel, la position d’un corps dans l’espace et sa quantité de mouvement (un vecteur) on pouvait calculer la trajectoire de ce corps qu’on appelle « géodésiques » (trajectoire du corps quand il ne n’est soumis qu’à la seule force gravitationnelle).

Le paramètre dynamique de cette trajectoire est le temps « absolu » newtonien, indépendant de toute chose.

Le principe d’équivalence stipulait que m_p = m_i, (expérience de Galilée à la tour de Pise) et le principe d’action réaction que m_a = m_p. Ceci faisait que les 3 types de masses étaient égales, avec un paramétrage convenable (en fait elles sont « proportionnelles »).

Cette force gravitationnelle à distance paraissait un peu mystérieuse, mais comme la théorie donnait de bons résultats, (on notait juste une petite anomalie pour l’avance du périhélie de Mercure qu’on pensait pour expliquer) seuls les esprits chagrins en étaient contrariés.

La relativité générale

Après la relativité restreinte en 1905, dès 1907, Einstein s’est intéressé à la gravitation, car il était convaincu que les principes qu’il avait utilisés devaient s’appliquer également à la gravitation.

Le problème était ardu et après des tentatives infructueuses utilisant le principe d’équivalence, il va s’intéresser à un autre type d’approche: une description géométrique permettant de définir la dynamique, à savoir les « géodésiques » suivies par les corps sous l’interaction mutuelle gravitationnelle.

Ces « géodésiques » ne seront plus des trajectoires, résultants de forces qui s’appliquent sur les corps en interaction dans un espace euclidien, qui ne sont pas des géodésiques, au sens géométrique, de l’espace euclidien, car les géodésiques de l’espace euclidien sont des droites.

Ce seront de vraies géodésiques d’une géométrie non-euclidienne.

Cela lui a pris 10 ans pour en arriver là, mais fin 1915 il va publier sa célèbre équation.

G_mn = k.T_mn.

G_mm est le tenseur d’Einstein , un objet géométrique dans un espace-temps à 4 dimensions (t,x,y,z), muni d’une métrique, définissant la courbure de la géométrie, k est une constante dimensionnée (liée à la force de Planck, voir pages de ce site) assurant l’homogénéité de l’équation et T_mn est un tenseur, le tenseur énergie-impulsion qui représente la « physique » (matière-énergie).

C’est cette équation qui va définir la structure de l’espace-temps résultant des propriétés d’une métrique (qui peut avoir des symétries) et la la matière-énergie qui la va contraindre.

Dans cette approche, toutes les masses et l’énergie contribuent à définir l’espace-temps auquel, en retour, toutes ces masses et toute cette énergie va se coupler et en décrire les géodésiques. Ceci inclut un auto-couplage implicite.

Ce sont donc les géodésiques de cet espace-temps (mathématiquement représenté par une « variété ») qu vont définir la dynamique du système.

En toute rigueur, doit-on considérer tout l’espace-temps ou seulement une catégorie de géodésiques?

Un problème se pose. Le modèle mathématique définit une un objet géométrique « une variété » qu’on peut considérer comme un ensemble de points sur lequel on peut définir n’importe quelle courbe. Mais la théorie, si on ne considère que la gravitation ne s’intéresse qu’aux géodésiques (et en plus une catégorie particulière).

Il parait donc naturel de ne considérer que la catégorie minimale de géodésiques, qu’on appellera géodésiques structurelles, qui définissent un sous ensemble des points de la variété, de façon structurée, car engendrées par ces géodésiques.

On sait les difficultés que présentent, par exemple la quantification. Mais en général les méthodes considèrent la variété globale, pas un sous ensemble beaucoup plus contraint ou on peut espérer que ce soit plus simple.

Il serait dont intéressant d’étudier ces possibilités avec un sous-ensemble aussi restreint que possible, car en toute rigueur, sous l’influence de la gravitation seule, ce qui est l’objet de l’équation d’Einstein, seules ces géodésiques et le sous-ensemble de points qu’elles définissent peuvent être utilisés.

Exemple de la solution de « Schwarzschild »

Ce cas est très simple car l’espace temps, ainsi défini, est vide: la seule masse au centre est une singularité. Comme E. Cartan l’avait déjà décrit, en 1922 [1], il existe deux classes (infinies) de géodésiques nulles, l’une radiale entrante, l’autre radiale sortante.

Ajoutons que pour réduire au maximum le sous ensemble on peut ne considérer que les géodésiques d’une fréquence donnée à l’infini, car pour des fréquences différentes, le paramètre affine (l’impulsion dans le cas des géodésiques nulles) induit des géodésiques différentes.

Ces classes définissent la structure causale de l’espace-temps et engendrent une partie des points de la variété à 4 dimensions (t, x, y, z) de manière structurée.

C’est ce que donne la solution de l’équation d’Einstein.

L’idée, c’est que ce sous ensemble restreint soit un sous ensemble minimum qui cependant capture (possède et permet de définir) toutes les propriétés de la solution à l’équation d’Einstein.

Faut-il aussi ajouter les géodésiques radiales entrantes et sortantes de type temps (double infinité), sans boost, qui génèrent d’autres points de manière structurée de l’espace-temps, bien décrites dans la solution de Painlevé (1921) ?

En toute rigueur, s’il n’y a pas de matière, on peut se demander si c’est nécessaire. Si on n’étudie que les géodésiques nulles, ce n’est pas nécessaire, sinon il faudra faire cette extension.

On peut se demander s’il existe des géodésiques de type espace structurelles, sachant que ce type de géodésiques ne sont pas considérées dans notre monde physique.

Les classes sélectionnées définissent l’espace temps restreint généré par un corps unique, à symétrie sphérique. On peut utiliser ce sous-ensemble, qui bien que multiplement infini, est bien plus restreint que celui qui serait généré par l’ensemble des points avec l’ensemble des courbes possibles.

L’espoir est qu’il se prêterait mieux à des opérations de quantification et autres opérations mathématiques.

Notons que la quantification opère une restriction par une contrainte, opération similaire à celle que nous proposons, par une contrainte également.

Toutes les autres solutions (géodésiques circulaires, non circulaires, quelconques et les lignes d’univers non géodésiques ) ne sont pas des solutions « natives » de l’équation d’Einstein, car elles nécessitent des éléments étrangers à la gravitation.

Quantification de l’équation géodésique

Puisque, comme nous l’avons soutenu, la solution de l’équation d’Einstein peut se limiter à l’équation géodésique, le problème se ramène à quantifier l’équation géodésique, ce qui plus restrictif que de quantifier l’espace-temps de manière générale. Voir la solution de Painlevé, par exemple:

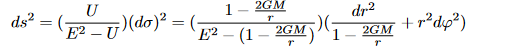
voir : https://astromontgeron.fr/Painleve-article-english.pdf

pour plus de détails.

Exemple du modèle standard de la cosmologie.

Dans ce cas l’univers n’est pas vide, puisque le tenseur matière énergie n’est pas nul. En plus des géodésiques nulles il faudra considérer les géodésiques de la matière « co-mobile » de l’expansion.

Toutes les autres lignes d’univers, géodésiques ou non ne relèvent pas nativement de la solution donnée par l’équation d’Einstein.

Là encore, un sous ensemble réduit génère tous les points nativement possibles de la variété. Le même type de remarques que précédemment s’applique.

Quid des géodésiques non structurelles et les lignes d’univers non géodésiques?

On peut, bien entendu, aussi traiter des géodésiques non structurelles et des lignes d’univers non géodésiques, mais il faut bien comprendre que cela va se faire, en général [2], par un couplage « perturbatif » (sans influence sur l’espace-temps) entre des phénomènes, de nature non gravitationnelle, par exemple des boosts, dans un espace local en un point de la variété avec l’espace-temps (représenté par la variété) défini par l’équation d’Einstein, d’où la structure de fibré, dont l’espace-temps est la base et l’espace local, la fibre.

Ceci va rendre possible des courbes passant par d’autres points (t, x, y, z) de la variété à quatre dimensions (une extension).

En général on assimile tout cela à la relativité générale, mais ce n’est pas rigoureux, et à ce titre peut être la source de confusion voire d’erreurs.

Une réflexion complémentaire serait utile.

Annexe: Exemple de tentative de quantification en RG

Introduction

On connait la difficulté de réaliser cette opération dans le cas général. Les différentes approches (cordes, boucles,..) ne donnant pas vraiment de résultat satisfaisant.

Nous proposons un certain nombre d’hypothèses pour aborder le problème.

A- L’équation d’Einstein définit des géodésiques.

1. L’équation d’Einstein définit un espace-temps, qui est généralement représenté par une variété, qu’on considère dans son intégralité.
2. Nous soutenons que seules les géodésiques, concernent la relativité générale. 
3. Cette approche d’Einstein, pour définir la dynamique d’un système, à savoir les trajectoires suivies par les constituants du système, se démarque de la méthode classique où des forces gravitationnelles, dans un espace de fond plat (Minkowskien en relativité,) agissent sur des objets pour leur faire décrire des trajectoires courbes (non géodésiques dans cet espace plat dont les géodésiques sont des « droites »).
4.  L’idée originale d’Einstein est de considérer que ces courbes, qui définissent la dynamique du système, sont des géodésiques d’un espace courbe, dont la courbure est régie par les objets.
5. En effet la relativité générale nous enseigne que toutes les masses et autres objets physiques contribuent à définir cet espace-temps auquel, en retour, elles se couplent en suivant des géodésiques. Donc, comme seules les géodésiques sont concernées par la relativité générale, nous ne considérerons qu’elles pour ce qui concerne l’équation d’Einstein. Des mouvements non géodésiques impliquent des interactions autres que celles prises en compte par l’équation d’Einstein.

B- Une analyse de type  » fréquentiel« 

D’autre part comme nous avons eu l’occasion de le décrire dans d’autres articles (http://www.astromontgeron.fr/SR-Penrose.pdf) nous considérerons que les géodésiques nulles sont les plus essentielles (elles définissent la causalité par exemple) et nous nous placerons dans ce référentiel de type nul, en rupture avec la méthode habituelle de références par un référentiel local de Minkowski.

 Ceci va nous amener à manipuler des fréquences au lieu de grandeurs spatiales et temporelles, de manière semblable à la représentation issue de transformées de Fourier.

C- Importance des géodésiques principales nulles

Dans les géodésiques nous considérerons les géodésiques principales qui jouent un rôle structurel essentiel pour définir le type d’espace-temps (classification de Petrov-Pironi, par exemple.

D- Cas de la solution de Schwarzschild

Fort de toutes ces hypothèses nous allons considérer le cas simple de l’espace-temps de Schwarzschild. Ce cas simple n’est pas forcément représentatif de tout ce qui peut exister en relativité générale, mais il peut nous éclairer sur des pistes à suivre.

Dans un premier temps, compte-tenu des symétries, nous nous intéresserons à la géodésique nulle principale radiale entrante. Nous verrons si l’application de la méthode à la géodésique principale nulle sortante apporte des éléments nouveaux.

E- Trous noirs physiques

Les trous noirs physiques que nous considérons, résultant d’effondrements stellaires ne sont pas « parfaits » (le modèle décrit des trous noirs éternels, ce qu’ils ne sont pas, en particulier, la formation de l’horizon et la singularité centrale ne sont pas achevés. Ceci fait, entre autres que la « singularité centrale » n’est physiquement pas « singulière » de même que l’horizon n’est pas une surface pure.

Pour l’horizon, nous savons (cf Penrose) que dans l’effondrement d’une masse en trou noir, même si l’horizon met un temps infini pour être une surface, il existe avant cela un phénomène de « surface » on devrait plutôt dire de région « piégée », qui n’est pas infiniment mince mais qui fait que la matière en effondrement dans cette région est vouée à finie dans la « singularité en devenir au centre. Nous savons que l’extension analytique maximale inclut un symétrique du trou noir.

F- Extension analytique maximale

Le cas des trous noirs maximaux avec région symétrique en expansion.

Ce cas, réputé non physique (on ne connait pas de processus de formation), sauf s’ils on été formés dans un univers très primordial sur lequel on ne sait pas grand-chose, présente un intérêt théorique toutefois car l’énergie d’un tel système symétrique, évalué par l’intégrale de Komar, par exemple, donne un résultat (théorique) nul. Cela suggère le vide et, sur le modèle du vide quantique dont l’énergie n’est pas nulle, on peut construire une version quantique du système, qui, peut-être, n’inclut pas de « singularité ».

Ceci pourrait être étudié également.

G-Quel décalage spectral dans la solution de Schwarzschild ?

Le décalage spectral s’entend entre une fréquence émise par un observateur en un point donné et sa mesure par un autre observateur situé en un autre point.

Il convient donc de préciser quels observateurs nous allons considérer. Ils seront tous situés sur la géodésique principale radiale et seront caractérisés par la valeur de la coordonnée r.. L’émetteur de la fréquence f = f₀ sera supposé à l’infini (en théorie), à une coordonnée r = r₀ = constante >> r_s , où r_s = 2GM est le rayon de Schwarzschild. L’observateur qui reçoit et mesure cette fréquence et trouve f = f₁, se trouve à une coordonnée r= r₁.

H- Cas d’observateurs « statiques »

Si on considère des observateurs « immobiles », associés à la métrique de Schwarschild, (statique), alors le décalage spectral ( pour r₀ = infini) est donné par l’équation :

 f₁ = f₀ [1-2 GM/r₁ ]^1/2]^-1

Qui, quand r₁ >> 2GM, (observateur statique qui fait la mesure de fréquence est loin de l’horizon) se réduit à:

f₁ = f₀ (1+ GM/r₁ )

C’est une équation « similaire » à celle de la mécanique newtonienne.

On sait que l’équation du mouvement pour des particules physiques en chute libre radiale, sans boost, depuis l’infini, dans ces conditions, est la même qu’en mécanique newtonienne.

Par contre, cette concordance avec la mécanique newtonienne s’arrête quand on se rapproche de l’horizon. La figure 1, où l’équation du cas général est représentée, montre que le photon entrant dans cette forme n’atteint jamais l’horizon à l’approche duquel, sa fréquence mesurée par un observateur statique (dont l’accélération qu’il subit tend vers l’infini) , tend également vers l’infini.

I-Cas d’observateurs en chute libre radiale sans boost.

La représentation, dans la forme de Painlevé (stationnaire), par exemple, suggère que l’espace-temps vide n’est pas statique mais en effondrement radial. En fait les observateurs « de Painlevé, en chute libre radiale sans boost » n’ont pas réellement de vitesse, ils sont co-mobiles de l’effondrement de cet espace.

Si à l’infini, le cas est le même que celui du paragraphe précédent, dans ces conditions la mesure f =f₁ (de la fréquence f=f₀, émise à r₀ = infini), par un observateur de « Painlevé,» situé en r₁,  en chute libre radiale géodésique sera différente.Elle est donnée par l’équation:

 f₁ = f₀ [1+(2 GM/r₁ )^1/2]^-1

J-Pertinence physique des 2 cas

Pour synthétiser, le cas décrit en H correspond à une mesure dans un espace de fond « statique ». Il suppose des observateurs statiques qui ne sont pas géodésiques donc qui n’appartiennent pas à la solution donnée par l’équation d’Einstein qui ne traite que de la gravitation, donc d’éléments géodésiques. En effet il reste à déterminer par quel procédé, nécessairement non gravitationnel) les observateurs statiques (qui subissent une accélération) sont dans cet état.

Le cas décrit en I correspond à une mesure dans un espace stationnaire en effondrement. Les observateurs qui effectuent la mesure de la fréquence sont géodésiques donc en accord avec l’équation d’Einstein. Il s’ensuit que si on veut caractériser la solution d’espace-temps, ce cas est représentatif de la phénoménologie de cette espace-temps.

Diagramme synthétisant les deux cas.

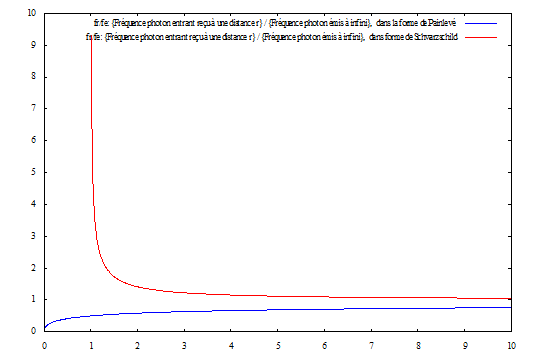
Fig. 1 : En abscisse la coordonnée r , (r = 2GM =1) et en ordonnée le rapport f₁/f₀

Ce diagramme confirme clairement combien les phénoménologies de la variation de la fréquence en fonction de l’endroit de sa mesure (caractérisé par la valeur de la cordonnée r), pour un rayon entrant, défini par sa fréquence à l’infini, lumière qui suit une géodésique principale nulle, de ces deux modèles, sont très différentes, ce qui est normal, car elles correspondent à deux conceptions très différentes de l’espace-temps.

Un photon radial entrant n’atteint jamais la singularité (physique) centrale dans le formalisme de Painlevé.

Les équations et la figure 1 associée, montre que dans le cas de la forme, réputée représentative de l’espace-temps (Painlevé), la fréquence du photon entrant, s’il travers l’horizon (singularité de coordonnées fictive) sans problème, n’atteint pas la singularité centrale. En effet, pour r₁ = 0, sa fréquence, mesurée par un observateur géodésique co-mobile de l’espace, est nulle. Comme un photon de fréquence nulle n’existe pas (ici n’existe plus) il « s’évanouit » et n’atteint pas r =0.

Ce point est intéressant car la présence d’une singularité, sans horizon pour s’en protéger, (censure cosmique), fait craindre une faillite de la physique, par exemple de la causalité. Si à l’extérieur de l’horizon la physique était protégée par cet horizon, on pouvait se poser la question de la validité de la physique quand on l’a franchi, puisqu’aucun autre horizon, dans cette solution n’existe!

La propriété résultant des équations, du cas jugé représentatif de la description de cet espace-temps, la description par la forme de Painlevé, par exemple, est rassurante sur ce point, car dans l’exemple de la lumière, les géodésiques ne sont pas connectées à la singularité, ce qui doit les prémunir contre ses effets néfastes.

[1] Petrov et Pironi, retrouveront et complèteront la contribution de E. Cartan, bien plus tard.

[2] Dans l’espace temps de Kerr-Newmann, l’espace-temps global est défini par le couplage de 2 équations, celle d’Einstein et celles de Maxwell, ceci échappe au cas général puisque cette contrainte est globale.

Note: Dans les équations, on pose c = 1, où c est la vitesse de la lumière. On la rétablit, si nécessaire, par cohérence dimensionnelle. Ainsi quand on écrit r_s = 2GM, il faut lire : r_s = 2GM/c².

à suivre…