On dynamics, in gravitation
What interests the scientist are the laws of motion of bodies in mutual gravitational interaction: the dynamics of a system. Indeed it is always the action of a phenomenon that we are interested in.
Newtonian mechanics
Newton, who located these bodies in a three-dimensional « absolute » Euclidean space (which therefore serves as a reference), assigned to each body an active mass ma, generating a « gravitational field » extending into this space according to laws he specified, a passive mass mp, characterizing the coupling of the mass with the field generated by the other masses (but not by his own: no self-coupling). He also assigned an inertial mass mi, according to the famous law f = m i.a. where a is the acceleration that the body undergoes, mi, its inertial mass and f the « force » applied to the body.
This « invisible » force” f, exerted at a distance in a vacuum, derived from a scalar potential (therefore additive), which made it possible to easily calculate the potential generated by distant masses at any point. Knowing this potential, the position of a body in space and its momentum (a vector) we could calculate the trajectory of this body called « geodesics » (trajectory of the body when it is subject only to the gravitational force).
The dynamic parameter of this trajectory is Newtonian « absolute » time, independent of everything.
The principle of equivalence stipulated that mp = mi, (Galileo experiment at the Tower of Pisa) and the principle of action reaction that ma = mp. This made the 3 types of masses equal, with a suitable parameterization (in fact they are « proportional »).
This gravitational force at a distance seemed a little mysterious, but as the theory gave good results, (there was just a small anomaly for the advance of the perihelion of Mercury that we thought to explain) only the sorrowful spirits were upset.
General relativity
After special relativity in 1905, as early as 1907, Einstein became interested in gravitation, as he was convinced that the principles he had used should also apply to gravitation.
The problem was difficult and after unsuccessful attempts using the principle of equivalence, he will be interested in another type of approach: a geometric description to define the dynamics, namely the « geodesics » followed by the bodies under the mutual gravitational interaction.
These « geodesics » will no longer be trajectories, resulting from forces that apply to interacting bodies in Euclidean space, which are not geodesics, in the geometric sense, of Euclidean space, because geodesics of Euclidean space are straight lines);
They will be geometric geodesics of non-Euclidean geometry.
It took him 10 years to get there, but at the end of 1915 he published his famous equation.
Gmn = k.Tmn.
Gmm is Einstein’s tensor, a geometric object in a 4-dimensional spacetime (t,x,y,z), provided with a metric, defining the curvature of geometry, k is a dimensioned constant (related to planck’s force, see pages of this site) ensuring the homogeneity of the equation and Tmn is a tensor, the energy-impulse tensor which represents « physics » (matter-energy).
It is this equation that will define the structure of spacetime resulting from the properties of a metric (which can have symmetries) and the matter-energy that will constrain it.
In this approach, all the masses and energy contribute to defining the spacetime to which, in return, all these masses and all this energy will couple and describe the geodesics. This includes implicit self-coupling.
Therefore, it is the geodesics of this spacetime (mathematically represented by a « manifold ») that will define the dynamics of the system.
Rigorously, should we consider all spacetime or only a class of geodesics?
There is a problem. The mathematical model defines a geometric object « a manifold » that can be considered as a set of points on which one can define any curve. But, the Einstein equation which is related to gravitation only, will select some physical geodesics among all the curves (a specific class).
Therefore, it seems natural to consider only the minimum class of geodesics, which will be called structural geodesics, which define a subset of the points of the manifold, in a structured way, because generated by these geodesics.
We know the difficulties presented, for example, in quantification. But in general, the methods consider the global manifold, not a much more constrained subset where one can hope that it is simpler.
Therefore, it would be interesting to study these possibilities with the convenient smallest subset because, rigorously, submitted to the gravitation alone, which is the object of Einstein’s equation, only these geodesics and the subset of points they define will be used.
Example of the « Schwarzschild » solution
This case is very simple because the spacetime, thus defined, is empty: the only mass at the center is a singularity. As E. Cartan had already described, in 1922 [1], there are two (infinite) classes of null geodesics, one radially incoming, the other radially outgoing.
Let us add that to reduce the subset as much as possible we can consider only the geodesics of a given frequency at infinity, because for different frequencies, the affine parameter (the momentum in this case of null geodesics) induces different geodesics.
These classes define the causal structure of space-time and generate a subset of the points of the 4-dimensional manifold (t, x, y, z) in a structured way.
This is what the solution of Einstein’s equation says.
The idea is that, even though, this minimum subset covers only a small part of the manifold, nevertheless, it would capture (provide and allow to define) all the physical properties of the solution to the Einstein’s equation.
Should we also add the incoming and outgoing radial timelike geodesics (double infinity), without boost, which generate other points in a structured way of space-time, well described in the solution of Painlevé (1921)?
Strictly speaking, if there is only vacuum, one may wonder whether it is necessary.
We may also wonder if there are structural spacelike geodesics, as this class of geodesics are not considered in our physical world.
The selected classes define the restricted spherically symmetrical spacetime. We can use this subset, which although multiplely infinite, is much smaller than that which would be generated by the set of all points obtained with the set of all possible curves.
The hope is that this restrictive subset would help to quantization and mathematical improvements.
Note that quantization operates a restriction by a constraint, an operation similar to that which we propose, by a constraint also.
All other solutions (circular, non-circular, any geodesic and non-geodesic worldlines) are not « native » solutions of Einstein’s equation, because they require non gravitational phenomena.
Quantization of the geodesic equation ?
As, per our assumption, that the geodesic equation alone will define the useful physical spacetime provided by the Einstein equation in this solution, the problem is quantization of the geodesic equation. A smart solution was given by Painlevé in 1922.
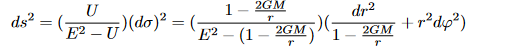
see : https://astromontgeron.fr/Painleve-article-english.pdf
for more details.
Example of the standard model of cosmology.
In this case, the universe is not empty, since the momentum-energy tensor is not null. In addition to null geodesics, it will be necessary to include the geodesics of the matter « co-mobile » of the expansion.
All other worldlines of the universe, geodesic or not, do not natively match the solution given by Einstein’s equation.
Again, a reduced subset generates all the natively physically possible points of the manifold. The same type of remarks as before applies.
What about non-structural geodesics and non-geodesic worldlines?
We may, of course, also deal with non-structural geodesics and non-geodesic worldlines, but we must understand that this will be done, in general [2], by a « perturbative » coupling (without influence on spacetime) between phenomena, of a non-gravitational nature, for example boosts, in a local space at a point of the manifold with space-time (represented by the manifold) defined by Einstein’s equation, hence the fiber structure, of which space-time is the base and the local spaces, the fibers.
This will make possible physical curves passing through other points (t, x, y, z) of the four-dimensional manifold (an extension).
In general, all of this is related as general relativity, but this is not rigorous, and as such can be the source of confusion or even errors.
Appendix: Example of a search for a quantization of GR
Introduction
We know how this is difficult in the general case.The current different approaches (strings, loops, etc.), even though some improvements in our knowledge, are not fully satisfactory. We propose a number of hypotheses to address the problem.
A- Einstein’s equation defines only geodesics.
1. Einstein’s equation defines a spacetime, which is generally represented by a manifold, which we consider as whole entity.
2. We argue that only geodesics, concern general relativity.
3. This approach of Einstein, to define the dynamics of a system, namely the trajectories followed by the constituents of the system, stands out from the classical method where gravitational forces, in a space with a flat background (Minkowskian in relativity, ) act on objects to make them describe curved trajectories (non-geodesic in this flat space whose geodesics are “straight lines”).
4. Einstein’s original idea is to consider that these curves, which define the dynamics of the system, are geodesics of a curved space, whose curvature is driven by all the matter and energy.
Indeed, general relativity teaches us that all masses and other physical entities contribute to define this spacetime to which, in return, they couple by following geodesics.
So, as only geodesics are concerned with general relativity, we will only consider them in the Einstein’s equation as non-geodesic motions, which imply interactions other than gravitation, are not taken into account by Einstein’s equation.
B- We suggest a “frequency” analysis
On the other hand, as we had the occasion to describe it in other articles (http://www.astromontgeron.fr/SR-Penrose.pdf)
we will consider that the null geodesics are the most essential (they define the causality for instance). Therefore, we will consider null geodesics reference frames.
This breaks with the method of using a local Minkowski reference frame, but, as exhibited by the Newmann-Penrose formalism, this is very efficient for grasping the structural properties of the spacetime.
This will lead us to manipulate frequencies instead of spatial and temporal data, this being similar to the representation resulting from Fourier transforms.
C- interest of null principal geodesics
Among all geodesics we will select the principal null geodesics which play an essential structural role in defining the type of spacetime, see Petrov-Pironi classification, for instance.
D- Case of the Schwarzschild solution
With all these assumptions we will consider the simple case of Schwarzschild spacetime. This simple case is not necessarily representative of everything that can exist in general relativity, but it can inform us on a way to follow.
At first, taking into account the symmetries of this spacetime, let us select the incoming radial principal null geodesic.
We may also review later, if this method applied to the outgoing null principal geodesic brings new elements.
E- Physical black holes
The physical black holes that we consider, resulting from stellar collapses ( and further collisions) are not « perfect » (the theorical model describes eternal black holes, which they are not. Especially, the formation of the horizon and the central singularity are not fully finished.
This makes, among other things, that the « central singularity » is not physically really « singular » just as the horizon is not really a surface.
For the horizon, we know (cf Penrose) that in the collapse of a mass into a black hole, even if the horizon takes an infinite time to be a surface, there exists before that a phenomenon of a « trapped » region, which is not infinitely thin but which means that the collapsing matter in this region is doomed to end in the « central mass”, itself in progress of becoming a singularity.
F- Maximum analytical extension
In addition, we know that, even though, the maximum analytic extension of the theorical model includes a mirror image of the black hole (expansion), this is not the case in physical black holes, unless they were formed in a very primordial universe, an poorly known era.
They would nevertheless be of theoretical interest however because the energy of such a symmetric system, evaluated by the Komar integral, for example, gives a (theoretical) zero result.
This suggests vacuum and, on the model of the quantum vacuum whose energy is not zero, one can build a quantum version of the system, which, perhaps, does not include a “singularity”.
This could also be studied.
G-Spectral shift in the Schwarzschild solution?
The spectral shift is defined between a frequency emitted by an observer at a given point and its measurement by another observer located at another point.
It is therefore appropriate to specify which observers we are going to consider. They will all be located on the radial worldline and at a value of the r coordinate.
The frequency f = f0 is emitted at “(infinity, in theory)”, in fact, at a coordinate r = r0 = > > rs , where rs = 2GM is the Schwarzschild radius.
The observer, at a coordinate r= r1, receives and measures this frequency and finds f = f1
H- Case of « static » observers
If we consider « static » observers, associated with the Schwarschild’s metric, (static), then the spectral shift ( for r0 = infinite) is given by the equation:
f1 = f0 [1-2GM/r1]1/2]-1
which, when r1 >> 2GM gives :
f1 = f0 (1+ GM/r1)
This equation is « similar » to that of Newtonian mechanics.
We know that the equation of motion for physical particles in radial free fall, without boost, from infinity, is the same as in Newtonian mechanics.
I-Case of observers in radial free fall without boost (called, sometimes, fiducial observers).
The representation, in the form of Painlevé (stationary), for example, suggests that spacetime (vacuum) is not static but in radial collapse.
In fact, the “Painlevé’s observers « , in radial free fall without boost » have, in fact, no velocity, they are just co-mobile of the collapse of this space.
Even though, at infinity, the situation is the same as that of the previous paragraph, the measurement f =f1 (of the frequency f=f0 emitted at r = r0 = infinite), by a “Painlevé’s observer,” located at r1, not static but in radial free fall, will be different. It is given by:
f1 = f0 [1+(2GM/r1)1/2]-1
J-Physical relevance of the 2 cases
Static observers are not compatible with the native (involving only gravitation) solution of GR and should lead to a misunderstanding of the structure of this spacetime
The case described in H corresponds to a measurement in a “static” background space. This implies static observers which are not geodesic observers and therefore not part of the solution in general relativity which involve only geodesics.
This case should be discarded.
Geodesic observers are compatible with the native GR solution (involves only geodesics)
The case, described in I, is a co-mobile measurement in a collapsing stationary space.
The spacetime solution described by this case is representative of the phenomenology of this spacetime as this needs no background fictitious spacetime and no static observers which are not geodesic.
Diagram summarizing the two solutions.
This diagram confirms that the phenomenology of the frequency shift per the location of its measurement (the coordinate r), for an incoming ray of light which follows a null principal geodesic is very different for these two models.
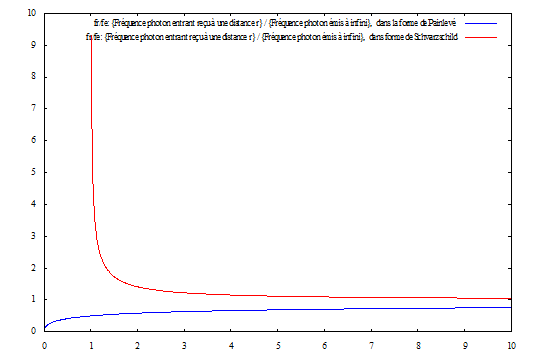
Fig. 1: On the abscissa the coordinate r , (r = 2GM =1) and on the ordinate the ratio f1/f0.
In the case of the static observer, the situation, for this null principal geodesic, is roughly identical to that of Newtonian mechanics but only for r1 >> 2GM as shown on the figure 1. When approaching the horizon at rs = 2GM , the phenomenololgy becomes very different. The energy of the photon becomes infinite and never reach the horizon.
But this case would not describe the structure of the spacetime as it requires static non geodesic, observers and suggest a backgroung static flat spacetime.
A radial incoming photon never reaches the central singularity in the Painlevé’s formalism
In other the case, that of geodesics observers, described by the Painlevé’s form of metric, as shown on figure 1, the photon cross invard the horizon (fictitious singularity), but the energy of the photon vanishes at the central (physical) singularity. In other words this means that it never reaches the singularity, this corroborrted by the fact that a photon, with a zero frequency, no longer exists.
This is an interesting structural property showing that the central physical singularity would not break the physics, for instance the causality, for this phenomenology as the singularity is out of range for photons.
Definitely this case is more representative of general relativity.
To be continued…
[1] Petrov and Pironi, will find and complete the contribution of E. Cartan, far much later.
[2] In Kerr-Newmann space-time, global space-time is defined by the coupling of 2 equations, Einstein’s and Maxwell’s, this is an exception of the general case since this constraint is global.
Note: In equations the velocity of light c is set to 1. For instance, 2GM represents 2GM/c².