Causalité et orientation en relativité générale
De manière générale en relativité, il est impossible de définir une simultanéité universelle, et de dater les évènements de manière universelle. La relativité a opéré un tel carnage dans nos concepts de temps et d’espace que nous croyions intangibles qu’on peut se demander ce qui reste et comment une physique peut être définie sur un tel champ de ruines ! Comme on pouvait s’en douter, elle n’a pas tout détruit car il reste possible de définir une causalité, ce qui est essentiel en physique, entre deux évènements A et B par des critères.
La règle est que l’évènement A a pu être la cause de l’évènement B, si et seulement si, un signal lumineux émis de A au moment de l’évènement A, atteint B, avant ou au moment où l’évènement B se produit. C’est la vitesse finie de la lumière qui fournit le critère.
On utilise souvent une représentation géométrique faisant intervenir un cône de lumière avec ses deux nappes de part et d’autre du sommet associé à l’évènement. En fait c’est un hypercône, mais pour la représentation on supprime une dimension d’espace. Notons que la forme du cône de la figure 8 s’étend à l’infini en relativité restreinte, mais que, en relativité générale, cette forme est locale, valide près du point A, et que son extension, au-delà, sur une ligne d’univers, est en général déformée par rapport à la figure.
Ce cône définit trois régions, la région du passé de l’évènement A qui est la partie intérieure du cône inférieur où se trouve C, avant l’évènement A, qui a pu être la cause de A, la région du futur de l’évènement A qui est la partie intérieure du cône supérieur, après l’évènement A, où se trouve B qui a pu être causé par A et la région qu’on appelle « ailleurs » à l’extérieur des deux parties du cône où se trouvent D qui n’a pas pu être la cause de A et E qui n’a pas pu être causé par A.
Dire que B est postérieur à A, suppose qu’une orientation passé-futur de A vers B soit définie. Comme indiqué, sur la figure, par la coordonnée t, l’intérieur du cône du haut est le futur de A, l’intérieur du cône du bas est le passé de A.
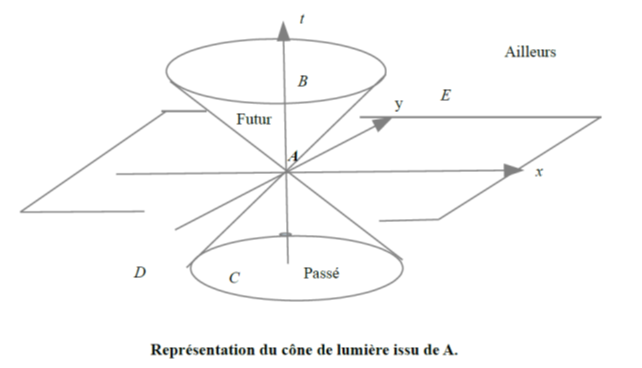
Figure 8 : Cônes de lumière et causalité en relativité
Cette notion de causalité associé à l’orientation donne un critère d’ordonnancement des événements, donc permet de définir une chronologie, à partir de sa structure interne, associée à l’humain qui y réside et fournit l’orientation qui est celle de son temps propre.
Comme, indiqué, en relativité générale, ce cône est déformé. Sa représentation dépend des coordonnées utilisées. Il existe des cas où la région du passé recouvre la région du futur: cette pathologie est caractéristique d’un situation où la causalité est violée. B. Carter a étudié cette pathologie dans la solution que R. Kerr a donné pour les trous noirs en rotation où il existe une région (la Carter Time Machine) comportant des boucles temporelles et permettant même de « remonter le temps » (du moins, selon la solution théorique).
Ce cas assez rare est plutôt déconcertant, si sa réalité physique n’a pas été démontrée, son impossibilité ne l’a pas été également, même si certaines conditions de symétrie, associées à la solution de Kerr, semblent physiquement difficiles à respecter, (formation de l’horizon interne).
Quelques autres conséquences de l’existence d’une vitesse maximale finie
Notons que cette vitesse finie implique d’autres propriétés :
- Voir loin, c’est voir dans le passé, puisque la lumière met d’autant plus de temps à nous parvenir que l’objet qui l’émet est éloigné.
- L’orientation temporelle définissant par exemple que B est dans le futur de A est donnée, comme nous l’avons annoncé dans l’introduction, par l’orientation du temps propre des observateurs sur leurs géodésiques, en l’occurrence l’observateur qui serait en A.
Soulignons toutefois, qu’à part ce cas, introduire un observateur pour décrire certaines propriétés des géodésiques est fait pour des raisons pédagogiques, mais que les géodésiques et lignes d’univers sont des courbes dans un espace-temps qui possèdent intrinsèquement ces caractères spatiaux et temporels.
C’est sur la structure interne de l’espace-temps relativiste que cette orientation va s’appliquer : L’orientation ne résulte pas d’un paramètre temporel extérieur global qui serait le paramètre dynamique de l’univers de sa création à son futur dont le présent serait notre présent.
Le rôle structurel de vitesse de la lumière imposé par le principe de relativité
En mécanique classique la lumière et sa vitesse ne joue aucun rôle structurel. C’est quelque chose qui se déplace à grande vitesse mais il n’est pas plus particulier qu’un autre objet en mouvement.
En relativité, c’est très différent.
D’abord soulignons que ce n’est pas la lumière, en tant que phénomène physique, qui joue un rôle particulier, mais le fait que pour satisfaire au principe de relativité, une vitesse particulière, commune à tous les référentiels, existe. Ceci apparaît en relativité restreinte quand on impose que les lois régissant les phénomènes physiques doivent être identiques dans tous les référentiels inertiels et que les transformations entre référentiels forment un groupe. Cette vitesse commune est une limite supérieure pour tous les phénomènes physiques [1].
Rappelons que, par définition, cette vitesse v est la vitesse d’un référentiel inertiel A de coordonnées internes x’, t’, mesurée dans un autre référentiel inertiel O, évaluée dans ce référentiel inertiel O avec ses coordonnées internes, x et t où v = x/t [2]. Cela est localement aussi le cas en relativité générale.
La valeur de cet invariant de vitesse n’est pas spécifiée par ces contraintes, mais son existence l’est. Il y a alors deux cas, soit cette vitesse est infinie, alors on retrouve la mécanique newtonienne (la forme du ds² de la relativité restreinte est dégénérée dans ce cas), soit elle est finie (peu importe sa valeur) auquel cas on obtient la relativité restreinte.
C’est l’existence de cette vitesse finie qui détruit le temps universel et l’espace absolu et lui substitue l’espace-temps.
Il se trouve que les ondes électromagnétiques (la lumière entre autres) et les ondes gravitationnelles ont les propriétés (une masse nulle, une nature de type fréquentiel) pour posséder cette célérité. Ce sont des marqueurs physiques de ces contraintes.
Ainsi quand Einstein a posé les deux postulats de la relativité restreinte, il aurait pu formuler le deuxième ainsi : « Il se trouve que la vitesse finie commune, déduite du principe de relativité est celle, constatée expérimentalement, de la lumière ! »
Indépendamment du rôle de cette vitesse commune dans la causalité, d’autres conséquences structurelles s’en déduisent qui montrent que cette propriété va bien au-delà de la définition de la causalité, même si aujourd’hui nous n’en avons pas une vision très claire.
Par exemple le formalisme de Newmann-Penrose [25] qui décrit l’espace-temps de la relativité (restreinte et générale) par rapport à la lumière, par une base de vecteurs nuls, est particulièrement efficace pour montrer les symétries des phénomènes, ceci se traduisant par des équations bien plus simple,s pour décrire cet espace-temps, que celles issues du formalisme standard (base spatio-temporelle).
La vitesse finie de la lumière qui est une limite de vitesse de propagation de n’importe quel signal ou interaction induit le concept de localité. Des changements locaux sont liés à une interaction locale.
Une diversité importante peut exister car la modification n’est pas immédiatement connue et ne provoque pas immédiatement de réaction de tout l’univers. Un univers isolé où les interactions seraient instantanées serait très différent.
[1]Cette limitation laisserait à penser que la distance qu’un observateur physique de A pourrait parcourir dans B est limitée par sa durée de vie par exemple, ce n’est pas le cas, car le paramètre à prendre en compte pour la durée de vie est le temps propre de l’observateur A, qui n’est pas la coordonnée t et qui peut tendre vers zéro (le temps de A, vu de B ne s’écoule plus) lorsque la vitesse v se rapproche de celle de la lumière c. C’est un des « paradoxes » de la relativité.
[2] Nous considérons un référentiel A où la vitesse de A est parallèle à la coordonnée x de B. On peut aussi considérer l’inverse, la vitesse de A dans B, la vitesse serait v’ = x’/t’ = -v.