Introduction: The Tsiolkovski equation
The classical Tsiolkovsky equation gives the increase in speed ΔV of a rocket during the phase of propulsion. Let us stress that has been established in the co-moving frame of the rocket by integrating a local equation of momentum conservation. In Newtonian mechanics, time and space being universal, this result was universal, unlike in relativity where time and space depend on observers.
Relativistic Tsiolkovski equation
The Rocket frame
Established in the co-moving frame of the rocket, its dynamic parameter is the astronaut’s proper time, measured by his watch.
The increase of the “proper” velocity of the rocket ΔV is measured by integrating the data of inertial devices such as gyroscopes which will define this parameter among all the trajectory’s parameters.
The ground frame
For the observer at rest, on the ground, it is with the time t, given by his watch (its proper time is different of that in the rocket), and the space x, given by a previous measurement of space of his frame of reference denoted R, that the observer will evaluate the speed v = dx/dt, of the rocket, which is tangent to the curve x(t) describing its trajectory from the ground.
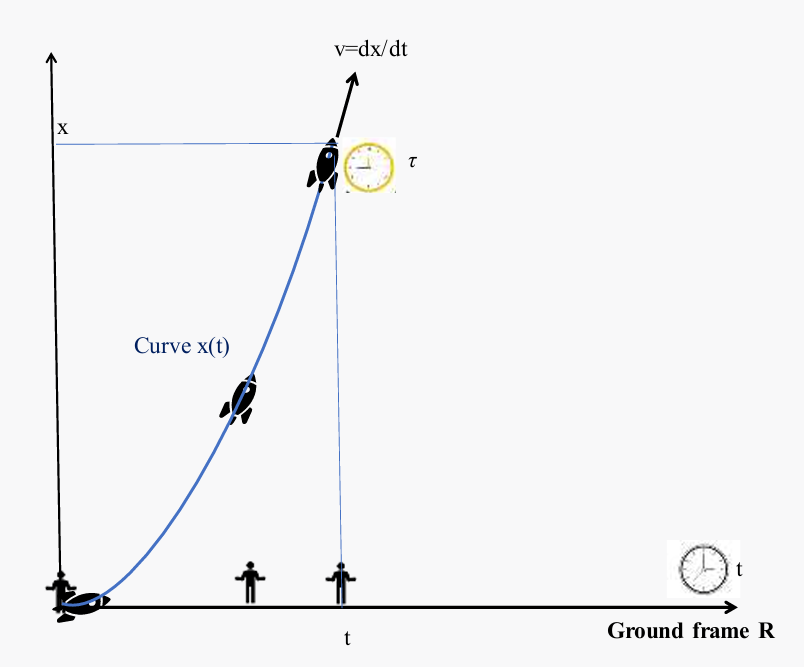
For an accelerated motion, the general relationship (with c = 1) between these parameters is given by a relationship like:
t = a -1 sinh(a.τ) , x = = a -1 cosh (a.τ) (1)
where t, x are the coordinates of the ground frame denoted R, a is the proper acceleration and τ is the proper time of the observer in the rocket.
Equation (1) is used in Rindler coordinates for a constant acceleration. But as the rocket has an acceleration which is not constant during propulsion step (is a function of τ ), we have to replace a by a(τ). As this equation (1) is valid locally, for the increase of velocity, we will, then, get:
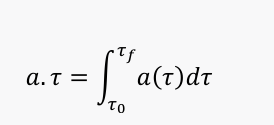
Physically, the value of this integral will be given by integrating the data provided by the inertial devices (i.e gyroscopes), exactly as in the classic Tsiolkovski equation, this providing, obviously, the same result. We do not have to solve this integral as we know its result.
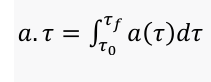
= ΔV= ve ln(mi /mf )
The rocket in the ground frame
Consider this equation (1), at the end of the propulsion. The speed in the ground frame R is:
v = dx/dt
let us differentiate (1)
dx = sinh (aτ)dτ, dt = cosh(aτ)dτ
this gives
v=dx/dt = tanh(aτ) (2.1)
where
aτ = V=ve ln(mi /mf ) (2.2)
V is the speed acquired in the frame of reference of the rocket, obtained by integrating the proper acceleration during the proper time τ of propulsion (principle of inertial navigation).
By plugging (2.2) in (2.1), with c, in R we get:
v /c= tanh[(ve /c)ln(mi /mf )] (3)
This is the relativistic Tsiolkovski equation
Convergence with classic Tsiolkovski equation when v/c << 1
Per the Taylor serie of tanh (x), if v << c, at first order of (ve/c), we get
v/c ≈ (ve /c) ln(mi /mf )
which is the classical Tsiolkovsky equation.
Limit for infinity proper velocity
For V=ve ln(mi /mf ) tending to infinity we get
v /c= tanh[(ve /c)ln(mi /mf )] —> 1, because tanh (infinity) = 1
Rindler formalism and horizon
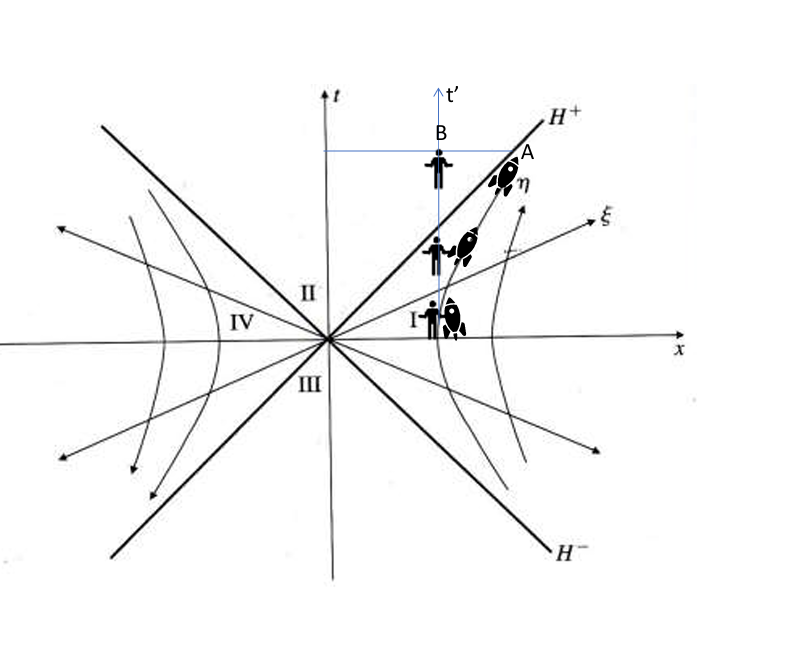
This phenomenology will include event horizons. Let us use Rindler coordinates, which are well suited for describing this type of phenomenology. When the rocket is at A, it is beyond the horizon for observer B who has remained stationary in the initial frame of reference.
Another demonstration, chapter « Special relativity » on the link:https://en.wikipedia.org/wiki/Tsiolkovsky_rocket_equation
By Jacques Fric, PHD history and philosophy of sciences- Paris Cité university