Expansion of the universe
We observe that all galaxies move away from each other all the more rapidly the more they are distant, the more the light emitted from the objects is redshifted the more they are distant and the interval between two events also undergo temporal dilation.
All of these phenomena are interpreted by assuming that space is « expanding », within the framework of the Robertson-Walker metric. The phenomena described are objective and the intention is not to question them.
But, beyond the mysterious nature of this phenomenology (a space that expands), this is based on a foliation of spacetime in time and space, (by using some coordinates) which, even if it is judicious, is arbitrary.
We know that in relativity, time and space taken separately have no physical character, the latter being the prerogative of space-time
In any case, there would be no more reason to attribute a physical character to the space defined in this way than to another defined according to another foliation using other coordinates. This interpretation is therefore not universal. Another way, more consistent with general relativity, to describe this phenomenology is to say that celestial objects describe the geodesics defined by Einstein’s equation, which is undeniable, and that this particular structure is an “internal” property. of spacetime and not of space, and that if we observe these properties in space, it is due to the experimental process of observation and its interpretation.
This is explained in the book “Vous avez-dit Big Bang”.
Expansion acceleration: Cosmological constant
This acceleration, which is observed experimentally, is generally attributed (this is by no means definitive, but for the moment it is the hypothesis most consistent with experimental findings) to the presence of a cosmological constant in the universe that ‘we try to justify by “the energy of a vacuum” despite a huge difference in scale. We discuss this difference in other articles on this site, especially about the Planck force. If the physical interpretation is still open to question, the geometrical context must be specified, because let us recall the relativity which underlies cosmology is a geometrical theory of gravitation.
The cosmological constant alone defines a four-dimensional spacetime with maximum symmetry (10 symmetries). null it corresponds to Minkowski’s spacetime (special relativity), positive to a De Sitter spacetime and negative to an anti-De Sitter spacetime. They are all spacetime where the spacetime curvature, represented by the Ricci scalar is constant. This implies that the Riemann tensor, depending on the metric and its first and second derivatives; from which the Ricci scalar is produced by a double contraction has a very particular form: it does not include any derivative of the metric. Without going into details, this is the difference of 2 tensorial product of the metric.
The metric is described in coordinates, one of which is timelike and has the opposite sign (in the metric) to those of the spacelike ones. We then understand that for the expression to remain constant when we traveling on a worldline of the universe where time is increasing, space,of opposite sign must also increase to keep the curvature constant. Of course, you have to do the math, with the mathematical formula that describes these expressions, to be convinced, the argument having an analogical character for the phenomenon.
Expansion of the universe or divergence of geodesics in the manifold representing the universe?
The cosmological constant alone defines a four-dimensional space-time with maximum symmetry (10 symmetries), zero it corresponds to Minkowski’s space-time (special relativity), positive to a De Sitter space-time and negative to a space -time anti- De Sitter.
They are all space-time where the spatio-temporal curvature, represented by the Ricci scalar is constant. This implies that the Riemann tensor, depending on the metric and on its first and second derivatives from which the Ricci scalar results from a double contraction, has a very particular form: it does not include any derivative of the metric.
Without going into detail, this is the difference between 2 tensor products of the metric. The metric is described in coordinates, one of which is time type and has the opposite sign (in the metric) to those of the space type. We then understand that for the expression to remain constant when traversing a universe line where time is increasing, the space of opposite sign must also increase to keep the curvature constant. Of course you have to do the math, with the mathematical formula that describes these expressions, to be convinced, the argument having an analogical character for the phenomenon. Certainly, by doing so, we proceed by analogy to describe the phenomenon. You have to do the math, with the mathematical formula that describes these expressions, to be convinced.
The congruence of geodesics defines the internal structure of the universe
We will show by a simple calculation how to show that, rather than talking about the expansion of the universe, it should be considered as an internal property of this universe. For this we will consider the congruence of geodesics in the Robertson-Walker metric. This congruence describes how a bundle of geodesics, around and in the vicinity of one arbitrary geodesic, behave when the affine parameter of this arbitrary geodesic varies.
This will describe the internal structure of the geometry of the manifold representing space-time (the universe) because the Einstein’s equation essentially describes the dynamics of gravity characterized by the geodesics in this geometric theory of gravitation.
For a given orientation of the variation, its circular section can vary (expansion / contraction), deform (shear) or rotate (rotation). This information is described by parameters, in particular the expansion (or contraction) parameter, generally designated θ, of the congruence which is a scalar and which is the only non-zero parameter, in this form of metric. It is written:
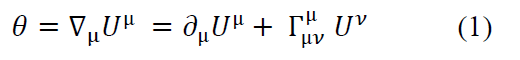
The sign « nabla » (triangle on the tip) represents the covariant derivative. Equation (1) is the covariant divergence of the 4-geodesic vector Uµ of components (t, r, θ, φ), conventionally noted respectively, 0, 1, 2, 3, whose components are:

Under these conditions, since only U0 is not zero, equation (1) is written:
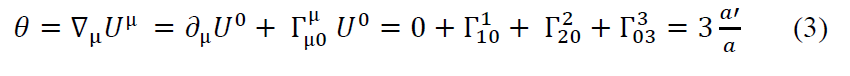
The partial derivative of U0 is zero because U0 = 1, and the Christoffel symbols are:
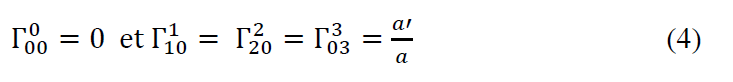
And a ’denotes the derivative of a (t) with respect to t. Taking, for example, the solution given by Friedmann’s equations with k = 0 gives:
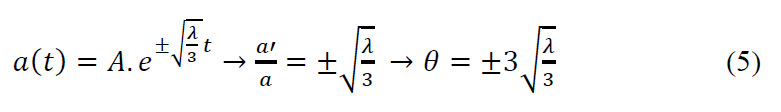
This expansion θ, constant in the case of a De Sitter universe, is therefore, intrinsically, geometric. Geodesics describe the internal structure of this geometry, independently of all the physical interpretations that can be considered.
This constant expansion of the bundle of geodesics leads to an exponential expansion.
Case of a non-empty universe
When there is momentum-energy in the universe (cold matter, relativistic matter and radiation), one can wonder, when this quantity of energy matter tends towards zero, what “naked” geometric structure would come and be the frame of such a space-time. The usual assumption is that the curvature is zero so that a space-time would tend towards Minkowski’s space-time when matter-energy tends towards zero.
But it can just as well tend towards a De Sitter or anti-De Sitter space which has the same level of symmetry. Is there a reason to favor one or the other? For example, if the cosmological constant turns out to be the right solution for our universe, there is no reason to be surprised, all solutions are equally symetric.
Primordial inflation
This paradigm, rather well integrated today in the cosmological model, assumes that, very early in the history of the universe, an exponential-type growth took place for a time equal to at least 100 times the age of l universe, at the time it occurred. This explains a number of phenomena observed on the homogeneity of the universe, the horizon problem, the near zero curvature of the spatial section in the Robertson-Walker metric and the absence of magnetic monopolies.
The horizon problem
The study of the CMB (cosmic microwave background) shows that it is very homogeneous (the inhomogeneities are of the order of 10-5). In a medium, for example a gas, the homogeneity results from the numerous collisions between the atoms which leads to a thermal equilibrium which follows a law of the black body type.
For this to happen, the different parts of the universe must have been in contact. Without this inflation, in the standard model, except very specific initial conditions, this seems impossible.
Note that this is a physical phenomenon since it is the limit beyond which no more signals reach us. In a dynamic universe this limit depends on cosmological time, unlike the horizon in the Schwarzschild solution with black hole where it is fixed.
The problem of zero curvature of space
An argument put forward is that to account for this quasi-nullity of this curvature, it would have required extraordinarily particular initial conditions, and therefore extraordinarily unlikely. The argument is interesting, but it should be noted that the “flatness” of the spatial section of a spacetime is not universal, because this space depends on the foliation of space-time in time and space. which itself depends on the coordinates.
Thus, for a De Sitter space-time for example, there exist solutions where the space section is positive, negative or zero, for the same space-time, (described mathematically by the same manifold), some covering the entire variety of others only a part, depending on coordinates.
We can therefore be doubtful about the intrinsic value and the importance of these zero curvature for the spatial section which has no physical character.
Our interest in solutions without cosmological constants was undoubtedly linked to the fact that the fate of the universe depended on this curvature (closed, open, asymptotically infinite).
But with the cosmological constant, the situation has changed.
Validation of the inflation paradigm
To be validated, this paradigm must be the subject of experimental verifications. While it is true that it solves several problems, avoiding an extraordinarily particular initial conditions nevertheless as the Big Bang is itself a not really ordinary event and if we accept it, we might not be surprised that ‘it is accompanied by another unlikely event.
It appears that this paradigm has gone through many versions since the beginning and that many variations exist and are part of research today.
The quantum scalar field mediator “the inflaton” is unknown and if it was thought to be the Higgs boson, this hypothesis seems abandoned today.
In addition, the profile and the properties of the scalar field associated with inflation require significant constraints to represent the phenomenon as described, which means that if constraints as strong as those initial required for a universe of geometry spatial flatness, we do not see the benefit of adding this paradigm, unless it solves problems that the fine adjustment of the initial parameters does not solve (problem of the horizon, homogeneity, spectrum of fluctuations, absence of magnetic monopolies). Certainly, all of these points lend credence to inflation, but the current confusion and plethora of variations show that the story is far from over.
Only unambiguous experimental verification would lift the mortgage on this paradigm.