Introduction
Si on lance le pendule dans une certaine direction sur la Terre, le pendule de Foucault suit une trajectoire qui semble tourner par rapport au sol.
En fait, on constate expérimentalement, qu’au premier ordre au moins [1], nonobstant l’action gravitationnelle des astres « proches » (Terre, Soleil, Voie lactée,..), il bat dans une direction pointant, au loin, vers un point fixe par rapport aux quasars lointains qui sont les repères du balisage de l’univers dans sa totalité, utilisés en astrométrie.
Le pendule étant un instrument de type « inertiel », sa trajectoire est une géodésique, mais de quelle géométrie?
Si on décrit ce phénomène qui semble (au premier ordre) ne prendre en compte que l’univers entier, en relativité générale, ce sera alors une géodésique de la géométrie de l’univers, telle que décrite par le modèle standard de la cosmologie.
Cette rotation du mouvement du pendule par rapport au référentiel donné par la Terre constatée est donc apparente car le phénomène physique détecté est la rotation de la Terre, ceci à l’instar du mouvement apparent du Soleil dans le ciel qui n’est, également, que la manifestation de la rotation de la Terre.
Les dispositifs de type inertiel (pendule, gyroscopes, gyromètres, accéléromètres, ..) ont la capacité de détecter des accélérations « propres », dont celles liées aux rotations qui sont des phénomènes non inertiels, ces phénomènes « non inertiels » ayant un caractère intrinsèque, (lié à la dynamique de l’objet concerné lui-même) ne pouvant pas être « annulés » dans un référentiel inertiel.
Principe de Mach
Mach a stipulé au 19ième siècle que l’inertie [2] des corps résultait de leur interaction gravitationnelle avec tous les corps de l’univers. L’inertie était de nature gravitationnelle. En conséquence cela fondait le principe d’équivalence : masse inerte = masse pesante (masse gravitationnelle passive qui se couple au champ gravitationnel), puisque l’inertie était de nature gravitationnelle.
La relativité générale
En relativité générale tous les corps contribuent à la géométrie de l’espace-temps auquel, en retour, tous ces mêmes corps se couplent en suivant des géodésiques de cette géométrie. Sur le principe, on voit que cela va dans le sens de ce que Mach à stipulé.
On comprend alors que, le pendule est un instrument ayant un mouvement inertiel décrivant une géodésique, ce soit une géodésique de l’univers.
Pourquoi la direction ne change pas
Comme dans le modèle standard, l’univers est supposé isotrope en tout point, toutes les directions sont équivalentes, donc ce sont les conditions initiales qui vont déterminer une géodésique (parmi toutes celles possibles) dans l’univers, et il n’y a aucune raison physique pour qu’elle change, sauf à être perturbée.
Avant de passer à suite, considérons quelques autres instruments « inertiels, » permettant de détecter et mesurer des mouvements non inertiels.
Gyroscopes
Le gyroscope est un autre dispositif inertiel très utilisé. L’axe de rotation, d’une masse isotrope autour de cet axe de rotation et en rotation, en l’absence de perturbation, va pointer une direction fixe qui dépend des conditions initiales.
Accéléromètres et gyromètres
Accéléromètres
Cet instrument permet de détecter et mesurer des accélérations linéaires propres, par exemple, en utilisant l’inertie d’une masse, inclue dans le dispositif constituant l’accéléromètre, solidaire de l’accélération du corps.
Gyromètres
Ces instruments inertiels sont destinés à détecter et mesurer une rotation propre. On peut citer les gyromètres à fibre optique utilisant l’effet Sagnac pour leur précision.
Par rapport à quoi définit-on l’ accélération et la rotation propres?
On entend souvent à propos de la rotation d’un objet : Mais par rapport à quoi tourne un objet?
Cette question sous-entend une approche newtonienne avec un espace absolu de référence. En fait, la détection d’un mouvement non inertiel (accélération linéaire propre ou rotation propre) par un dispositif inertiel, (Pendule, gyroscope, accéléromètre, gyromètre,..), se réfère au corps lui même.
Par rapport à son état à l’instant t, si l’état immédiatement suivant à (t +dt) ne résulte pas d’un mouvement inertiel, indépendamment de toute référence extérieure, le dispositif va le détecter et éventuellement le mesurer.
L’exemple des trous noirs de Kerr en relativité générale
On peut se demander par rapport à quoi ces trous noirs dits « en rotation », par comparaison avec les trous noirs « statiques » de Schwarzschild par exemple, tourneraient.
Dans l’approche relativiste, comme un trou noir de Kerr définit un espace-temps complet (infini) effectivement, comme il ne tourne pas par rapport à lui-même, on peut être dubitatif.
En fait c’est la géométrie de cet espace-temps de Kerr, différente de celle des trous noirs « statiques » qui caractérise le phénomène de rotation.
Ainsi, par exemple, la géodésique d’un objet à l’infini, sans vitesse initiale tombant radialement, est une « radiale entrante », modélisée par une « ligne droite » pointant vers la singularité centrale (un rayon) dans la solution d’un trou noir statique, alors que le même objet, dans les mêmes conditions initiales va suivre des courbes, qu’on pourrait interpréter (de façon newtonienne) comme subissant une « rotation » alors qu’en fait il ne fait que suivre les géodésiques de cette géométrie .
La métrique de Kerr qui définit sa géométrie, qui contient un paramètre caractérisant cette rotation (un moment angulaire) est plus complexe de celle Schwarzschild, mais elle se ramène à elle quand ce paramètre est nul.
Situation physique
En fait cette condition d’homogénéité et d’isotropie que nous avons décrit pour expliquer pourquoi le pendule pointerait toujours une direction ne dépendant que des conditions initiales est une approximation à l’échelle de l’univers, mais localement, elle n’est pas totalement respectée [3] . Ceci entraine des effets locaux qui vont provoquer une infime déviation le la direction.
Exemple de mesure de la déviation géodésique dans un cas réel
Cela a été mesuré par l’expérience Gravity Probe B, [4] utilisant des gyroscopes ultra-précis qui ont montré une très faible déviation géodétique (liée à la courbure de l’espace-temps par la masse de la Terre) et une déviation « gravitomagnétique » (entrainement de référentiel) encore plus faible liée à la rotation de la Terre.
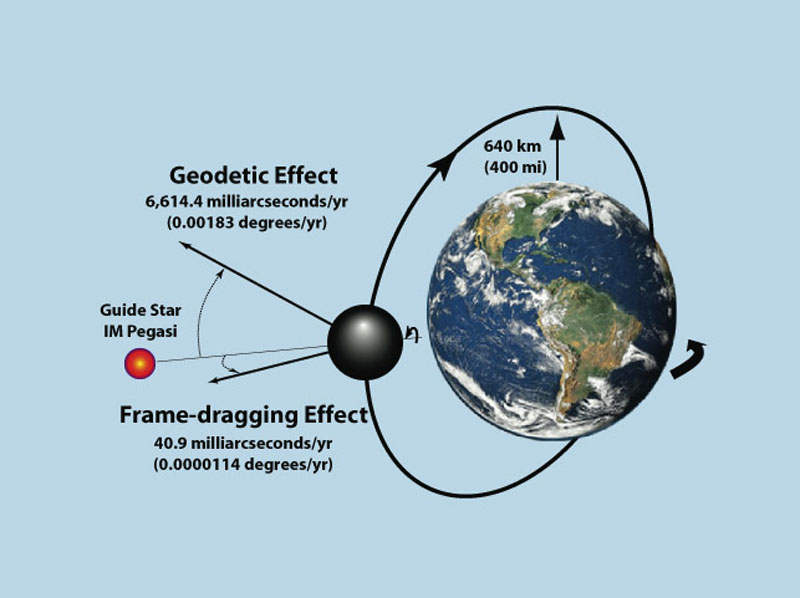
Article complet sur Gravity Probe-B, ci-dessous.
Notes
[1] En fait, comme l’univers n’est pas du tout homogène et isotrope localement, même si cet effet est faible localement pour la Terre et même le Soleil, la géodésique va subir localement d’infimes déformations par rapport à la géodésique d’un univers parfaitement homogène et isotrope.
Cet aspect du problème sera explicité dans la fin du document.
Insistons sur le fait que c’est bien la géodésique qui est localement déformée par rapport à la géodésique si l’univers était homogène et isotrope. La perturbation du mouvement du pendule, dispositif inertiel, est liée au fait que le pendule suit cette géodésique déformée localement.
Ceci peut être observé comme l’expérience « Gravity Probe-B » le montre (avec des gyroscopes) . Bien entendu, compte-tenu de la faiblesse de la perturbation, le dispositif inertiel doit être quasi-parfait et très sensible.
[2] L’inertie cette capacité des corps de résister à un changement d’état, un état inertiel se caractérisant par le fait que, ponctuellement ,aucune contrainte n’est ressentie.
[3] La géométrie locale n’est pas celle de l’univers global, par exemple autour de la Terre ce serait une géométrie décrite par la métrique de Schwarzschild avec un effet Lense-Thirring pour sa rotation.
[4] Pour l’effet géodétique, cela a été mesuré (et confirmé) avec une bonne précision, pour l’effet Lense-Thirring la précision est médiocre du fait de l’extrême faiblesse de la perturbation. Il semble que les auteurs de l’expérience aient un peu surestimé les performances des gyroscopes (réputés 10 fois plus performants que ce qui existait alors) qui ont été limites pour mesurer l’effet Lense-Thirring.
Bien entendu c’est parce que cet effet est très petit pour un astre comme la Terre, mais pour des étoiles à neutrons et encore plus pour des trous noirs de Kerr, où il existe une ergosphère, region entrainant inexorablement en rotation tous les éléments physiques y compris les photons, cet effet Lense-Thirring devient très important.
Certains ont même mis en doute la validité de la mesure, obtenue après de nombreux calculs destinés à éliminer les effets indésirables.
publié par J. FRIC